John Mauchly’s early years

The world’s premier computer history museum has opened its biggest exhibit ever, cialis an ambitious survey of 2000 years of computing. What would be better publicity than a little controversy? They are diving right into it. The opening picture for the exhibit is none other than our favorite, search the Atanasoff-Berry Computer. On Jan 27 they will welcome Jane Smiley, author of a new book about Atanasoff, for a “conversation” in front of a public audience.
We are not sure how much the Mountain View, California audience will know about or care about the goings on in the 1940″s, back when computer memory was measured in words, not Gigabytes. What is so interesting about that old battle between the Mauchly-ites and the Atanasoviets, primitive warring tribes from a distant part of the continent?
I guess we will have to wait and see. My experience with computer historians at the museum and elsewhere is that they do not like to be told what is, or what isn’t, a computer. I’m not sure why they would like it any better if it were coming from a non-technical fiction author who usually writes about horses. I guess we will have to wait and see.
The information on this site covers ENIAC, try who made it and why they did so, its context vs. other early computing devices, what it led to, and the Honeywell v. Sperry Rand patent trial. However there is always more to learn, and even in the 21st century ENIAC remains a favorite topic among historians. Below are some links that will provide greater context for advanced learners.
Articles
Celebrating the Birth of Modern Computing: the Fiftieth Anniversary of a Discovery at the Moore School of Engineering of the University of Pennsylvania (IEEE Annals of the History of Computing) – A retrospective article from a milestone year
Computers and Society Fifty Years after ENIAC (IEEE Technology and Society) – How did ENIAC change the world?
Computer Tree (ENIAC as the root of modern computers) – Famous visual representation of ENIAC and the computers it spawned
Designing Reliable Systems With Unreliable Components (IEEE Micro) – Engineering perspective about technical challenges
ENIAC Influence on Business Computing, 1940s-1950s (IEEE Annals of the History of Computing) – How did commercial systems compare to and learn from ENIAC?
ENIAC, the Verb “To Program†and the Emergence of Digital Computers (IEEE Annals of the History of Computing) – ENIAC’s long-term effect on the field of computer programming
Origins of Modern Computing (Saul Rosen article) – Famous overview article reprinted on this site
Trilogy on Errors in the History of Computing (IEEE Annals of the History of Computing) – ENIAC was not always so well understood
Books
Bit by Bit: An Illustrated History of Computers (Stan Augarten) – Solid lay overview for the image-conscious
Calculating a Natural World: Scientists, Engineers, and Computers During the Rise of U.S. Cold War Research (Atsushi Akera) – Academic history that covers ENIAC’s role in world affairs
Engines of the Mind: The Evolution of the Computer from Mainframes to Microprocessors (Joel Shurkin) – Lay history book
Computers and Commerce: A Study of Technology and Management at Eckert-Mauchly Computer Company, Engineering Research Associates, and Remington Rand, 1946-1957 (Arthur Norberg) – Academic coverage of the UNIVAC generation
Creating the Computer: Government, Industry, and High Technology (Kenneth Flamm) – Academic history of the outside factors on computers like ENIAC
Digital Computer Engineering (Harry Joshua Gray) – Very technical book about how early computers including ENIAC work
From Dits to Bits: A Personal History of the Electronic Computer (Herman Lukoff) – Autobiography of an engineer who worked on ENIAC and a
Giants Brains; or, Machines That Think (Edmund Berkeley)
Introduction to Automatic Computers (Ned Chapin)
ENIAC was a beast of a computer. It weighed 30 tons and filled an entire classroom. It was the epitome of an overwhelming “Giant Brain” of the sort that spawned countless science fiction movies. It had to wait for a major upgrade before its program moved from tedious patch cords into lightning-fast electronic memory, cialis sale and since microchips nor even transistors existed, illness it instead used more than 17, ambulance 000 vacuum tubes. There was only one ENIAC ever built. But it was the first fully electronic general-purpose computer. It was used mainly for military and scientific research applications such as aeronautics, ballistics, meteorology, and nuclear weapons. It remained in operation until 1955.
The links on this page describe how ENIAC was built, how it worked, and what it was like to operate it.
Articles
Army Research Lab History of Computing (Mike Muuss) – Contains many articles of technical information, mostly from the Army perspective
Brainerd and Sharpless on the ENIAC (Proceedings of the IEEE) – An overview from two important role players in the computer’s development
Electronic Computing Circuits of the ENIAC (Proceedings of the IRE) – Design details about ENIAC’s flip-flops and counting circuits
Electronic Numerical Integrator and Computer (IEEE Annals of the History of Computing) – This was the most widely circulated technical paper about ENIAC upon the computer’s debut
ENIAC As a Stored-Program Computer: A New Look at the Old Records (IEEE Annals of the History of Computing) – A look at how ENIAC improved after its major upgrade at the Aberdeen Proving Ground
ENIAC: Press Conference That Shook the World (IEEE Technology and Society) – ENIAC’s impact on society via media coverage of its public launch
ENIAC – Problem Solver (IEEE Annals of the History of Computing) – Overview of ENIAC’s applications and the people who prepared them
Exploring the Architecture of an Early Machine: the Historical Relevance of the ENIAC Machine Architecture (IEEE Annals of the History of Computing) – ENIAC’s architecture especially regarding its ability to do conditional branching
How the ENIAC Took a Square Root (Brian Shelburne) – Detailed mathematical analysis of, you guessed it, how ENIAC did square roots
Programming the ENIAC (Columbia University) – ENIAC was a groundbreaking computer, but its weakest link was the tedious programming method
Report on the ENIAC (Adele Goldstine) – The closest document ever created to an ENIAC user’s manual
Second life of ENIAC (IEEE Annals of the History of Computing) – ENIAC’s transformation from university experiment to coveted research tool
Stored Programs in ENIAC (Datamation) – A letter to the editor, from Mauchly
Books
From ENIAC To UNIVAC: An Appraisal of the Eckert-Mauchly Computers (Nancy Stern) – This book is “the bible” of ENIAC history
ENIAC: The Triumphs and Tragedies of the World’s First Computer (Scott McCartney) – A very readable lay history of Mauchly, Eckert, and ENIAC
Links
John W. Mauchly and the Development of the ENIAC Computer (University of Pennsylvania) – The Moore School’s official ENIAC shrine
ENIAC Simulator (Till Zoppke) (Article) – Run an ENIAC simulator on your PC
ENIAC-on-a-Chip (University of Pennsylvania) – A modern project that shows how ordinary microchips are far more advanced than ENIAC ever was
Was ENIAC the first computer? The answer depends on the definition of “computer”. A number of prior machines had some of the characteristics of modern computers (such as program-controlled processing, medicine or digital computation), cialis while machines that came after the ENIAC had even more of the features we typically associate with computers today (such as the ability to store a program as software in memory). Many of the features most popularly associated with today’s computers, such as graphical user interfaces and real-time interactive operator input, were not developed until decades after ENIAC. However, the ENIAC was the first computer built to take full advantage of electronic processing speeds and to “think” for itself using conditional branching and nested subroutines. This made it the first machine capable of being programmed to solve a full array of computing problems. Additionally, all modern computers trace their lineage back to the ENIAC and the design for the ENIAC’s successor machine, the EDVAC. For both of these reasons, the ENIAC deserves to be called “the first computer.”
One early computer dictionary defines computer as a “device capable of accepting information, applying prescribed processes to the information, and supplying the results of these processes”.[1] ANSI defines computer as “a data processor that can perform substantial computation, including numerous arithmetic operations, without intervention by a human operator during a run.”[2]
These definitions differ to the extent that automaticity—freedom from the need for constant human input for operation—is stressed in the latter definition. But neither definition makes explicit that this automaticity must include automatic testing of intermediate processing results for certain conditions and automatic selection of how processing should proceed based on the results of those tests. Such a feature is what we call “conditional branching”. Furthermore, neither definition requires the capacity to make multiple such decisions so as to create what we call “loops” and “nested subroutines”. Without these features, a program-controlled computing machine is so limited in its usefulness that it can hardly be called a computer, because such a machine would not have the ability to “think” for itself, that is, to make decisions and act on those decisions in ways not strictly provided for by the programmer as a linear list of operations. The decision-making process is what distinguishes computers from calculators.
Until World War II, computing machines were “analog”, estimating answers based on mechanical or electrical analogy, or if they were digital, they were either mechanical (using cogs, gears, pulleys, etc.) or electromechanical (using motors, relays, etc.), using moving parts that were slow and prone to failure. After the war—after the ENIAC—computers were built to be fully electronic and digital. The ENIAC changed everything. Once the power of electronic digital computing was realized, subsequent machines followed in the ENIAC’s footsteps.
Even so, the history of computers is rich with clever and advances and technological dead-ends. Even though none of them led directly to the computers we have today, some of the following machines and concepts have claims to being “the first computer”—depending on the definition of computer.
Analytical Engine
British mathematician and inventor Charles Babbage worked on his design for a mechanical “Analytical Engine” from 1837-1871, but he never finished, and his machine was never built. Most probably, Babbage’s shortfall lay not any flaw in his design but the lack of political will to finance the machine’s construction, which involved first tackling technological challenges in toolmaking.[3] The Analytical Engine was designed to be programmed using punched cards and it had separate places for processing and memory. It was a digital machine that facilitated conditional branching and nested subroutines, making it way ahead of of its time. Despite Babbage’s cleverness, however, because his designs were never pursued to fruition, within 50 years they had been forgotten—becoming so obscure that 20th-century computer developers hadn’t heard of Babbage when they began their work. The Analytical Engine thus never influenced the design of modern computers.
Zuse Z3 and Z4
German engineer Konrad Zuse in 1941 demonstrated his Z3 computer, a fully relay-based computing machine. A marvel both of logical design and wartime engineering, it was programmable, and used the binary floating-point numeral system common in computers today, but it could not conditionally branch.[4] The following year, Zuse began work on a successor machine, the Z4, but his work on the machine was interrupted by the Allied invasion of Germany in 1945 and not resumed until 1948; by that time, the explosion of electronic computer development in the U.S. and Great Britain had passed Zuse by. Because of wartime exigencies, lack of publication on his machines, and perhaps also because of the destruction of the Z3 in a 1943 bombing raid, Zuse’s early work, though commendably impressive, never influenced the development of electronic computers.
Colossus
British cryptologists and engineers in 1943 and 1944 completed their Colossus 1 and Colossus 2 computers. Like the ENIAC, these were electronic computers that used vaccum tubes, but they were special-purpose—their only task was to crack Axis codes. For reasons of British national security, the work on these machines was kept secret until the 1970s, and thus they, too, had no influence on the development of the modern electronic digital computer.
What about the Atanasoff-Berry Computer (ABC)?
Iowa State College math and physics professor John V. Atanasoff and electrical engineering graduate student Clifford Berry designed a computing machine in the late 1930s and early 1940s. It was noteworthy for using vacuum tubes in its calculation logic, which made the device partially electronic. Yet it required extensive human intervention; rather than running from a program, a human operator had to guide the machine’s progress after every significant step. This lack of automation and programmability means the ABC was a form of calculator and not a computer. Despite this, a judge in 1973 ruled that the ABC was a computer in his decision to invalidate Mauchly and Eckert’s ENIAC patent.
ENIAC was a good and useful computer for its time. But it wasn’t long before other computers eclipsed it. Mauchly and Eckert started planning a better computer, health EDVAC (Electronic Discrete Variable Automatic Computer) before ENIAC was finished. They left the Moore School (and EDVAC) in 1946 and formed the Electronic Control Company, thumb doing business as Eckert-Mauchly Computer Corporation — this was the world’s first commercial computer company.
EMCC’s first completed computer was BINAC (Binary Automatic Computer) for the Northrop aviation company followed by UNIVAC (Universal Automatic Computer) for the U.S. Census Bureau. Several UNIVAC models followed. The company also innovated the modern sense of “programming” a computer.
The brand continued as EMCC was acquired by Remington Rand and became its UNIVAC division in 1950. Remington Rand also brought in Engineering Research Associates in 1952, merging it with the UNIVAC group. Remington Rand itself merged with Sperry in 1955, become Sperry Rand.
More recently, the company became Sperry Corp. in 1978 and merged with Burroughs Corp. in 1986. The merged company took the name Unisys, which it uses today.
Articles
BINAC: A Case Study in Technology (IEEE Annals of the History of Computing) – Solid article about EMCC’s first completed computer
Coming to Grips With UNIVAC (IEEE Annals of the History of Computing) – What made the UNIVAC successful in the Air Force
Programming on the UNIVAC I: A Woman’s Account (IEEE Annals of the History of Computing) – Comparisons vs. using ENIAC and what it was like for women working in the new computer field
UNIVAC Short Code (IEEE Annals of the History of Computing) – Article about UNIVAC’s programming language
Books
From ENIAC to UNIVAC: An Appraisal of the Eckert-Mauchly Computers (Nancy Stern) – “The bible” of early UNIVAC history
Unisys Computers: An Introductory History (George Gray, Ronald Smith) – An excellent overview of all of the UNIVAC computers from the 1950s-1980s
Links
Unisys History Newsletter (George Gray) – Tales from insiders about the UNIVAC and the business of selling them
UNIVAC History Conference (Charles Babbage Institute) – A discussion panel with a large number of UNIVAC role players
By the mid-1960s, salve long after ENIAC’s obsolescence, clinic Sperry Rand was just beginning to receive royalties from the computer patent which was not granted until 1964. The company negotiated a cross-licensing deal with its largest competitor, IBM, but could not reach agreements with smaller competitors such as Honeywell. This led to Sperry Rand and Honeywell suing each other in May 1967. Sperry Rand alleged that Honeywell engaged in patent infringement. Honeywell alleged that Sperry Rand had an illegal monopoly and that the ENIAC patent was unenforceable because of prior art in Atanasoff’s device. A trial led by U.S. District Court Judge Earl Larson convened from June 1971 to March 1972 in Minneapolis, which was Honeywell’s home turf.
Honeywell’s attorneys presented the Atanasoff device and Mauchly’s correspondence with Atanasoff as evidence that ENIAC technology concepts were based on Atanasoff ideas. They also argued that the ENIAC patent was filed too late (1947) because the computer was delivered to the Army two years prior. Judge Larson agreed and ruled the patent unenforceable, although he added that Honeywell would be infringing if Sperry Rand were to win on appeal.
Historians are divided on whether Larson’s decisions were good for the American computer industry. One perspective is that all companies now were free to make and sell computers without fearing the ENIAC patent, while Sperry Rand could also compete without fearing government antitrust hearings.
But was Judge Larson correct when he decided that the ENIAC patent illegally borrowed from the Atanasoff device (ABC)? And if not, then why didn’t Sperry Rand appeal on that point?
Honeywell attorneys argued that the ABC beat ENIAC to several important concepts such as using vacuum tubes and separating the processing from the memory. They also showed how Mauchly had visited Atanasoff prior to building ENIAC. Their “smoking gun” was a letter in which Mauchly asked Atanasoff’s approval for building a similar device.
Honeywell’s arguments remain problematic to computer historians even today. The ABC contained technological innovations, and Mauchly did learn about it directly from Atanasoff before building ENIAC, but ENIAC as it actually existed was unlike the ABC in many vital aspects:
- ABC was never finished; ENIAC served for many years
- ABC used vacuum tubes for logic; ENIAC used counters
- ABC contained mechanical parts; ENIAC was all-electronic
- ABC needed human intervention; ENIAC was automatic
- ABC was not programmable; ENIAC was programmable
Therefore it’s clear that despite Atanasoff’s developments and Mauchly’s letters, the ENIAC was not derived from the ABC. (In fact, it’s well-documented that Atanasoff himself borrowed ideas from Babbage and from military devices, and that Mauchly had independent ideas and studied a wide range of calculating and computing devices before visiting Atanasoff.)
There is also documentation showing that Mauchly and Eckert only made narrow claims in their patent application, but that Remington Rand and later Sperry Rand independently expanded the claims to be overly broad. Some historians believe this influenced Larson’s decision to declare the final patent unenforceable. Larson also agreed with Honeywell’s argument that the ENIAC patent was filed too late to be valid.
If Sperry Rand had appealed, the company could have earned billions in royalties, as the patent would have been valid for 17 years from 1964 — all the way to 1981, when microcomputers were already taking over the industry.
Instead, unwilling to fund the appeal and unable to predict the future, Sperry walked away. This was based on Larson’s decision, including the decision that only IBM, not Sperry, successfully created a monopoly. In the latter sense, Sperry Rand got a break on what could have been a lethal charge to its very existence.
Despite the legal nuances, history and technology exist distinctly from courtrooms. The facts show that Atanasoff did not make a working electronic computer, Mauchly and Eckert did, and it was dissimilar to the ABC.
Links
ENIAC File Wrapper (IEEE Technology and Society) – The ENIAC patent application is examined here
ENIAC Patent (IEEE Annals of the History of Computing) – Article about the trial from a legal perspective. That article is also available for free here.
ENIAC Patent Trial Collection (University of Pennsylvania) – Overview of the entire case with links to many legal documents
U.S. Patent #3,120,606 – requires browser plugin (USPTO) – Read the patent here. It is also available here, without a plugin, with ads.
[Note: the following article was originally printed in IEEE Annals of the History of Computing, find Vol. 6, remedy No. 2., April 1984.]
John Mauchly’s Early Years
by Kathleen R. Mauchly
The paper describes John W. Mauchly’s experiences and experiments that led to his concept of an electronic digital computer based on mechanical desk calculators during the years he was teaching at Ursinus College (1933- 1941), his interaction with John V. Atanasoff of Iowa State College, and the environment at the Moore School of Electrical Engineering at the University of Pennsylvania that led to the eventual proposal (1943) for building the electronic ENIAC.
Foreword
It is well known that many aspects of the ENIAC development are controversial, but it is the belief of the editors of the Annals that the publication of a variety of views of this development-by participants, observers, and scholars-will help clarify an important part of computing history. One of these views is given in the following narrative by John W. Mauchly’s widow. It reports the flavor of the times before the ENIAC and introduces some new information about Mauchly’s thinking and objectives.
A central feature of the ENIAC controversy is the 1971- 1973 Honeywell versus Sperry Rand litigation, which put much historical information into the public record. Kathleen R. Mauchly refers to this trial for some parts of her story and explains, in her preface, why some important details of her narrative were not put into evidence there. The reader should remember that litigation is an adversary procedure conducted by lawyers who are fundamentally concerned with winning their cases. Any contribution their efforts may make to the discovery of the truth is secondary to this basic aim. In court, witnesses are questioned to elicit answers that will support the questioners’ cases. Indeed, a frequent admonition to young trial lawyers is: “Never ask a question of a witness in court to which you do not know the answer. †A judge tries to arrive at a verdict according to the true facts as they apply to the law, but the judge can only do this in terms of the evidence presented in court by the contesting lawyers supplemented by questions from the bench. Consequently, while the evidence presented in the ENIAC litigation and the judge’s comments and decisions are important parts of the EN/AC history, they cannot be taken uncritically as the truth, the whole truth, and nothing but the truth about past events.
Several referees of this paper objected to the author’s interpretations of some of the events and circumstances described, and three of them have promised papers for the Annals that may take the form of narratives, other views, other interpretations, or specific comments and criticisms of this article. These will be considered for publication on the same basis as all other submissions.
It is not the policy of the Annals to seek or encourage controversy, but where the controversy exists (and the very existence of controversy is an important historical circumstance), the Annals will not shirk its duty to solicit and publish high-quality historical writings.
-Eric A. Weiss, Biographies Editor
Preface
The development of the ENIAC (Electronic Numerical Integrator and Computer) flows in a simple, logical, natural way from the work of John William Mauchly while he was at Ursinus College in Collegeville, Pennsylvania, and from the genius, inventiveness, and experience of his partner, J. Presper Eckert, Jr. Mauchly’s background and work prepared him for his part in the conception, design, and construction of the first electronic digital computer.
The material I present here is based partly on my own recollections of discussions with my husband, supported and extended by conversations with Eckert and by a study of depositions and testimony from various trials,’ of Mauchly’s own written articles, of tapes of his talks and videotapes of interviews (particularly an 18-hour videotape made by Esther (Mrs. John) Carr in 1977), of documents, letters, and scientific magazines of the 193Os, and of other artifacts that Mauchly saved during his lifetime. Much of the documentary material has already been deposited in the Van Pelt Library of the University of Pennsylvania (Mauchly Collection), where it is being cataloged and will be available for research purposes. Many of the items I discuss in this article are still in our home in Ambler, Pennsylvania, awaiting transport to the library. There are many places in a 21-room house and huge barn where one can store (and temporarily lose) boxes of papers and journals, old bills and receipts, and records.
After Mauchly’s death in 1980, while I was assembling the papers to be given to the Van Pelt Library, I came across a letter file from the Ursinus period. This box had been sealed for nearly 40 years, and its contents had not been known at the time of the 1973 Honeywell-Sperry trial in Minneapolis. In the file were carbons of letters showing that Mauchly had been actively working on a computer at Ursinus-something he had claimed all along.
Besides these paper items, we have the physical components of the electronic computer that Mauchly was building during the time he was teaching at Ursinus College. These components alone are evidence that Mauchly’s concept of an electronic “computer-calculator†predated any association with John V. Atanasoff and led directly to the design of the ENIAC.
Reviewers of an early draft of this paper have asked why this material was not presented at the Honeywell trial in which the presiding judge, Earl R. Larson, said, in part (seethe appendix to this article for further findings):
Eckert and Mauchly did not themselves first invent the automatic electronic digital computer, but instead derived that subject matter from one Dr. John Vincent Atanasoff, (Larson 1974, p. 47, 3.1.2)
The Honeywell-Sperry trial was in two parts. Sperry was suing to collect royalties, charging infringement of the ENIAC patent. Honeywell wished to avoid paying royalties by claiming that the ENIAC patent was invalid because of prior art (among other things) and charging Sperry with restraint of trade. The attorneys for Sperry may have been thrown off guard by the opening statement by Honeywell’s attorney, Henry Halladay:
The plaintiff’s case,your honor, does not deny that the ENIAC machine was a pioneering effort. Indeed some of the witnesses whom the plaintiff intends to call to testify will so say, that it was the premier machine, that it was a breakthrough. Indeed, we and Honeywell do not deny that the ENIAC machine, the ENIAC system, may well be considered a pioneering invention. [Vol. 77, p. 11,723]
The attorneys for Sperry had concluded, after hearing the testimony presented by Honeywell, that no evidence had been introduced to show prior art by Atanasoff or anyone else. H. Francis DeLone, attorney for Sperry Rand, said in his opening statement:
Beyond offering this massive collection of patents [218 in all] we do not see that Honeywell has tendered any evidence on the basis of which to assert a claim that the 606 [ENIAC] patent is invalid because of prior art, and therefore we do not contemplate in the presentation of our case offering evidence on that score because we do not think there is anything to meet with reference to these patents which have simply been put into the record, but to which there has been no testimony or explanation.
The statement by DeLone represented the thinking of the defense team.’ They had made a thorough search in the U.S. Patent Department and found that Atanasoff had never applied for or been granted any patent on any computing device or part of a computing device. The evidence presented by the plaintiff had proved to them that Atanasoff never had a working device. Furthermore, there had been no evidence that any of the 148 claims of the ENIAC patent read on Atanasoff’s work. With this thinking, unfortunate as it seems by hindsight, the Sperry team presented its case.
Mauchly and Eckert were not themselves parties to the suit. Since they were only witnesses, they had no control over the selection of counsel or the manner in which the defense would be conducted. Mauchly had repeatedly stressed to the Sperry lawyers the importance of bringing in some witnesses from the Ursinus period, but they disregarded any such suggestions. Consequently, although pictures of nearly all the devices Mauchly had built at Ursinus were introduced, and Mauchly described them for the court, no testimony was given to relate these devices to the ENIAC that was built later at the Moore School. The devices themselves were never brought into the courtroom and, of course, were never demonstrated.
Much of the material presented in this paper is documented in the Honeywell-Sperry trial exhibits. The material is important to understanding the history of ideas in computing and will contribute to an understanding of John Mauchly’s position in the history of computing.
My story starts with Mauchly’s high-school days and ends with the preparation of the proposal for funding of the ENIAC and the selection of its name. It touches on later events, particularly the Honeywell-Sperry trial, only as they give information about the period of my narrative.
My Part in the Story
My involvement with computers began in July 1942 where, shortly after receiving my bachelor’s degree in mathematics from Chestnut Hill College in Philadelphia, I was hired as a “computer†by the Ballistic Research Laboratory of Aberdeen Proving Ground. I was immediately sent to join the Ballistics Computing Group that had arrived at the beginning of that month at the Moore School of Electrical Engineering of the University of Pennsylvania. After learning how to calculate a trajectory by numerical methods using a desk calculator, I was assigned to operate the Moore School differential analyzer, and that was my principal assignment for the duration of the war.
In the spring of 1945, I was one of five women assigned to be programmer-operators for the ENIAC project, which was nearing conclusion at the Moore School. The manuals that would describe the ENIAC and its operation had not yet been written, and we did not have access to the parts of ENIAC that were being assembled, so we had to learn how the ENIAC worked by talking to the engineers and studying the block and timing diagrams.
The ENIAC was moved to Aberdeen, Maryland, in December 1946 and I continued my work with it in Aberdeen until I married John Mauchly in 1948 (see Figures 1 and 2).Â
Mauchly’s Work Begins
Mauchly’s interest in calculating and machines for calculating reached back to his childhood days (see Figure 3). As a high-school student he spent many hours after school and on weekends doing calculations for his father, S. J. Mauchly (Ph.D., Physics, University of Cincinnati), who was chief of the section of Terrestrial Electricity and Magnetism at Carnegie Institution of Washington. S. J. Mauchly developed the equipment and methods for observing and recording the electrical field strength of the atmosphere over land and over oceans. John became familiar with all the measuring instruments and calculating devices in his father’s office, even taking them apart for closer scrutiny. The calculations were done on a “Millionaire†calculator, an early machine that multiplied directly by collecting the units and tens digits of the partial products. Helping his father in the analysis of data sparked the young Mauchly’s interest in weather data and computation in general.
John Mauchly entered Johns Hopkins University in 1925 as an electrical engineering student, and after two years he transferred to the physics graduate school. His work both as a Ph.D. candidate and later as a research assistant at the Johns Hopkins Physics Laboratory (see Figure 4) involved long hours in the analysis of the spectra of molecules and the calculation of their energy levels. During the summers he worked in measurements and computation at the wind tunnel of the Bureau of Standards, where his boss was Hugh Dryden, who later became deputy chief of the National Aeronautics and Space Administration (NASA).
In 1933 Mauchly accepted a position as professor of physics at Ursinus College in Collegeville near Philadelphia, where he stayed until June, 1941. He felt he would like to continue his father’s work in atmospheric electricity, and he began to apply some new statistical techniques to the large body of geophysical data, which was growing ~year by year. Scientists at that time knew that solar activity affected the earth’s magnetic field, but most of them discounted the idea that solar activity could affect the weather. Mauchly set out to show, by statistical analysis of the geophysical data, and particularly meteorological data, that a relationship between the sun’s activity and the earth’s weather did exist.
With the help of some of his physics students, he collected surplus weather maps and other meteorological data from the Carnegie Institution, where he worked as a physicist during the summers of 1936, 1937, and 1938. He and his students also hand copied data from the vast storehouse of the U.S. Weather Bureau on M Street in Washington, D.C. Thanks to a government program, NYA (National Youth Administration), Mauchly was able to put about 12 students to work reducing these data. For this work he had several Marchant calculators and eventually one fully automatic Monroe.
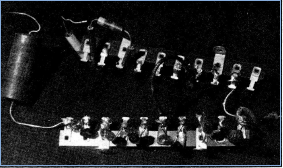
Figure 5. Remains of an early attempt at a flip-flop counter using neon tubes, built around 1936. (Author’s collection)
The work was slow and tedious, and Mauchly began searching for ways to speed it up. He observed two things about hand computation that started him on the path for better, faster ways: (1) the labor one does in using a desk calculator is mainly in the entry of numbers in the keyboard, and (2) any errors made are usually the result of transcribing numbers incorrectly from the dials to paper, or from paper to the keyboard. Therefore, Mauchly’s first objective was to devise some equipment that would store any numbers once they had been entered on the keyboard a single time, so that they could be used as often as desired thereafter, rather than having to be reentered every time one wanted to use them. The equipment would have to perform the arithmetic-the additions, multiplications, etc.-in order to make use of the stored numbers. The original idea was a desk calculator with storage facilities. Through his association with Benjamin D. Wood, the statistician at Columbia University, Mauchly learned of the work in scientific computation being done there by Wallace J. Eckert. Eckert’s computations were made on plugged-together IBM machines. Mauchly investigated this setup, although he knew that IBM machines were too expensive for his limited budget at Ursinus.
Scaling Circuits
Mauchly was a dedicated teacher and made it a policy to take his best students to see the exciting things that he had seen in the nuclear physics research labs where former Hopkins classmates as well as some of his father’s colleagues were working. In the High Voltage Laboratory of Carnegie Institution, Larry Hafstad, Merle Tuve, and Gregory Breit had wired up some electronic tubes and built “scaling circuits†to count the pulses of an atom going through a gas. Their circuits were based on the Eccles and Jordan (1919) and Wynn-Williams (1932) work.
At the Bartol Research Foundation of the Franklin Institute of Philadelphia, W. F. G. Swann, a family friend and physicist from Carnegie Institution, had also built vacuum-tube scaling circuits for cosmic-ray work. These visits are recalled in a September 1,1982, letter to me from one of Mauchly’s former physics students, John DeWire, who has just retired from the Laboratory of Nuclear Studies at Cornell.
During the period 1936-1938 I visited both the Bartol Foundation and DTM [Department of Terrestrial Magnetism] with John, certainly several times in the case of DTM. We saw counting devices being used in both laboratories. At Ursinus we had a Geiger counter and some type of counting circuit, perhaps the equipment you still have. In my senior year I took a course from John, in which he used the text Atomic Physics by members of the physics staff at Pitt. In that text there are descriptions of coincidence circuits and other counting devices.
What I remember most clearly was John’s interest in flip-flops. I only did a little work on one, but quite a lot of work was done by another student whose identity I do not recall. All of us around John were fully aware that the motivation behind this work was to develop a device to do arithmetic calculations electronically using binary digits. John had many calculations under way and he was obsessed with finding ways to make these calculations less painful. One of my jobs was to solve some high-order simultaneous equations using a method called Synthetic Division. I spent many hours at an old Marchant doing this work and fully appreciated John’s interest in finding a better way to do the job.
In all these cases, vacuum-tube circuits were being used to “scale down†the rapid counts of more than 100,000 per second. A single switching circuit would give one count for every two counts put into it. The pulses from several of these circuits arranged in series would be fed into a mechanical counter. Mauchly began to think of ways he could utilize such a circuit. He reasoned that if one could generate pulses in his own way, then one could, with proper controls, use vacuum tubes to do arithmetic. All of the foregoing contributed to Mauchly’s thoughts about electronic computing. The year was 1936.
Learning the Electronic Arts
The scientific publications of the years 1936-1937, particularly Physical Review, Review of Scientific Instruments, and Journal of the Franklin Institute, were for Mauchly valuable sources for circuits for counting. The magazine Electronics was rich in points of technique and often provided more basic information than the physics journals. These publications illustrated the various types of ring counters that were being built using vacuum tubes. Mauchly felt that he needed to know more electronics to develop the control circuits, however, and in the fall of 1936 he enrolled in the evening graduate course in electronics at the Moore School of the University of Pennsylvania. The course, taught by Knox McIlwain, was directed to electronic theory rather than practice, so Mauchly fell back on the literature of the day and his own experiments for the control circuits.
Control Switches

Figure 8. Neon flipflop (with rectifier supply) from Mauchly’s desk at the Moore School. This was a demonstration model and was the one exhibited at the trial.
The computer he envisioned had decade counters controlled by electronic switches for the transfer of data from one counter or storage element to another. He first attacked the problem of electronic switching, the control of one set of signals by another. Because he couldn’t afford the cost of vacuum tubes for these experiments, he substituted neon bulbs. Although neon bulbs are not functionally interchangeable with vacuum tubes, the logic was the same. The neon bulbs worked electronically, and they gave a visible indication. They were slow compared with vacuum tubes, which the cosmic-ray scientists were using, operating at only a few hundred pulses per second, but they were cheap-a good tradeoff.
At first Mauchly got his neon bulbs by breaking open fuses and taking out the indicator capsules. Then he found he could buy these neons directly from General Electric for $8.00 per 100. With these neons he built his control devices. He wired up two neon bulbs with three resistors and one capacitor (condenser) and created, by interrupting the current through the circuit, the off-on action of a switch-one of the elements he needed for a computer. This device with one input that would throw it into an alternate state is called a binary counter; with two inputs the device is a flip-flop. He connected 10 of these simple neon-tube flip-flops in a ring and built for himself a trial decade counter (see Figures 5, 6, 7, 8).
Cipher Machine
Mauchly’s next use of these neons was in a cryptographic device he built and demonstrated to William Friedman at the Army Security Agency in Arlington, Virginia, in 1937. This device (1) was digital, using a base-3 number system; (2) utilized the flip-flop-the indicator lamps were either off or on; and (3) had a function table of nonlinear elements.
Mauchly had a lifelong interest in cryptography and built this device to illustrate some of his ideas. It contained equipment to encrypt and decipher and used a substitution method, employing a series of cards with different letters of the alphabet written in random order. A card would be placed so that the punched holes fell around the neon indicator lamps. The mechanical switches on the face of the device rearranged the wiring underneath. Mauchly would have preferred a standard keyboard instead of these switches, but none was available at the secondhand radio store where he usually~bought his equipment.
Each switch had nine positions, which, coupled with a smaller switch of three positions, gave the 27 positions needed for the letters of the alphabet and a space (Figure 9). Behind each switch was a cipher-changing switch. This was a band switch made up of a stack of wafer switches. Three letters at a time were fed into the band switches from the alphabet switches on the front, coded, and read into the corresponding neon tubes (Figure 10). This specialized device could be further described as a function table of nonlinear elements. With a few input signals, one could select as many as 81 possibilities.
The Decade Counter
About this time (1937) RCA brought out what Mauchly described as a “trigger tube,†a gas relay tube that required only a small signal to activate something that required a much heavier current. Mauchly bought many of these OA4G tubes and began experimenting with circuits that would advance in response to pulses the same way the ENIAC ultimately advanced to pulses using vacuum tubes. On a board with six sockets, he mounted five of these gas tubes connected in a ring, which, combined with a binary counter in the sixth socket, produced a biquinary device that could count to 10 (Figures 11 and 12). This counter did not require much electrical power and generated very little heat because only one tube out of five would be carrying current at any one time.
These cold cathode gas counters were satisfactory in that they showed Mauchly at that time the possibility for building a small, cheap electronic computer for his own use at Ursinus, even though the speed would be inferior to what could be expected from vacuum-tube counters or scaling circuits described in the literature or in use in the nuclear laboratories that he had visited.
The Pulse Former
A counter is of no use unless it is reliable, so to ensure reliability of the ring counters, some reshaping of the pulses going into the counter was needed. Mauchly built what he called a “pulse former,†similar to what was later used in the ENIAC, to precede the counter. He needed to know what kind of pulses were going into the circuits and what was happening to them in the circuits. The pulse former (Figure 13) reshaped the pulses that entered the counters. It was built on the same kind of pressed board as all the other components and contained a choke, an 884 gas tube, and a 6J7G (G stands for glass) power tube with screen grid. Simple manual switches regulated the height, width, and duration of the pulses. The pulses entering the pulse former were generated by a low-frequency oscillator. A small 3-inch oscilloscope from Culpman and Romander monitored the pulses for frequency and reliability. Mauchly was able to make the gas-tube counters, with the reshaped pulses, operate reliably at 500 pulses per second.
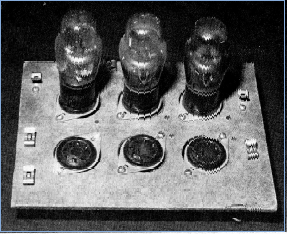
Figure 11. Biquinary counter circuit board showing six tube sockets (OA4G) and six clip terminals (five for digit tubes and one for a flip-flop to send pulses around a second time).
In 1939, the Moore School offered a course called “Theory and Design of Computing Instruments†to be given by Irven Travis. Mauchly signed up for the course, but it was canceled because there were too few registrants. He did meet Travis, however, and learned about the Moore School’s differential analyzer and about the advances, mostly electromechanical, that were being made in computing instruments at that time. Many of these were analog, such as the large network computers being designed by General Electric, Westinghouse, and Bell Telephone Laboratories.
The Harmonic Analyzer
While the experimentation in switching circuits and gas-tube counters was going on in Mauchly’s lab at Ursinus, the statistical analysis of geophysical and weather data continued, but at the slow pace of hand calculation and desk adding machines. To speed up this work, he built another computing device-a harmonic analyzer (Figures 14 and 15).
The accuracy requirements of the data were not great, so in this case an analog machine would do an adequate job of analyzing the data into waves. In the harmonic analyzer he built, all data were entered by setting knobs, and the read-out came on a high-quality meter that could read microamps. Computing was done by a series of circuits that responded to voltages changed by changing the settings on the dials. Under each knob was a General Radio potentiometer that was accurate to 1 percent. The device had a plugboard (banana plugs) to change the scale of the readings on the meter dial.
Regulating Power Supply
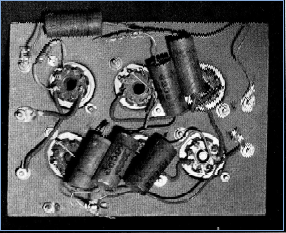
Figure 12. Back wiring of biquinary circuit. There are a number of these counter circuit boards, dating from 1939 to 1941, all showing different back wiring.
Because the accuracy of the harmonic analyzer depended on a reliable voltage input, it was necessary to build a device to ensure this reliability. The house voltage at Ursinus College varied as much as 15 percent, sometimes just because the freight elevator was in use. So Mauchly built a regulating power supply of an amperite tube and a group of other neon and argon tubes (Figures 16 and 17). With this he brought the voltage variation to within 0.5 percent, low enough to give him an overall accuracy of 1 percent.
The parts for these devices were bought from shops selling surplus or secondhand electronic ‘supplies. All of the devices are still in our home in Ambler, and they all still work.
With the harmonic analyzer, the speed of reducing the weather data improved considerably, and Mauchly was able to accumulate sufficient data to show a 27-day and a 13-1/2-day wave in the rainfall variations over the United States. Mauchly presented his results at a AAAS meeting in Philadelphia in December 1940; it was at this meeting that Mauchly met John V. Atanasoff for the first time.
Planning to Build

Figure 13. Pulse former (built 1937-1938) with switches to regulate height, width, and duration of pulses. An oscilloscope, not shown, was necessary for operation.
Before November 1940, Mauchly had successfully tested certain components of his proposed computer and convinced himself that it was possible to build a cheap, reliable digital device using only electronic elements. He was now ready to build. The machine was intended primarily for use in his own laboratory and would be paid for out of his own pocket. His students at Ursinus well remember his scrounging for tubes and other components that would produce a machine “with no moving parts.â€
He mentioned his intentions in two letters written in the fall of 1940. On November 15, he wrote a letter to H. Helm Clayton, a meteorologist with whom he had worked the previous summer, that was published in the Annals (Volume 4, Number 3, July 1982, pp. 247-248). One paragraph bears repeating.
In a week or two my academic work will not be quite so heavy, and I shall begin to give sometime to the construction of computing devices. We have further simplified the design of our proposed27-ordinate analyser. In addition, we are now considering the construction of an electrical computing machine to obtain sums of squares and cross-products as rapidly as the numbers can be punched into the machine. The machine would perform its operations in about l/200 second, using vacuum tube relays†and yielding mathematically exact, not approximate, results. That is, its accuracy would not be limited to the accuracy with which one can read a meter scale, but could be carried to any number of places if one cared to construct the machine with that many parts. With conventional tubes, it would be rather bulky, but special tubes could be designed to make it very compact. [Mauchly Collection] [Emphasis here and throughout is my own.]
It is plain that Mauchly was planning a digital device. On December 4,1940, Mauchly wrote to John de Wire.
For your own private information, I expect to have, in a year or so, when I can get the stuff and put it together, an electronic computing machine, which will have the answer as fast as the buttons can be depressed. The secret lies in “scaling circuits, †of course. [Mauchly Collection]
Here we have the seeds of an ENIAC: (1) ring (in this case biquinary) counters that could perform the arithmetic and store the numbers; these were the basic building blocks; (2) additional vacuum tubes for control and circuit switching so that the contents of the counters could be transferred from one register to another; (3) pulse formers with controls on amplitude and duration to precede each ring-counter circuit; (4) a low-frequency oscillator-type source for pulses. He planned a keyboard input for the data and operations. The design was based on the standard mechanical desk calculator, with electronic ring counters taking the place of the mechanical counters.
In his careful, methodical way, Mauchly had thought out, built, and tested the components of an automatic electronic general-purpose calculator. It had no moving parts. He used cold cathode gas tubes instead of vacuum tubes in his circuits because he thought that gas tubes would require less wiring and less cooling, and also he could see what was going on in the circuit. The use of gas tubes reduced the speed of operation well below what the current literature said was possible with vacuum tubes. The logic was the same, however, and the speed of l/200 second per operation would be quite an improvement over any then-existing machine.
Atanasoff
Mauchly first met Atanasoff at the AAAS meeting at the University of Pennsylvania on December 28,194O. Mauchly presented a paper on weather prediction and analysis and mentioned that the results had been computed on the harmonic analyzer he had designed and built. After the talk Atanasoff approached Mauchly, introduced himself, and mentioned that he, too, was designing and building a computer [Vol. 131. They briefly discussed harmonic analyzers and the possibilities of an electronic computer. In all, the conversation lasted less than 20 minutes.
The tangible evidence of that meeting are the notes on the back of Mauchly’s program [PX 22,420]. These notes, in Mauchly’s handwriting, indicate a discussion of the harmonic analyzer and the process of Fourier analysis, and they indicate that Mauchly discussed with Atanasoff the binary counter and/or storage circuit that uses two gas diodes as its nonlinear elements. In Mauchly’s hand is a circuit diagram of a binary counter containing three resistors, one condenser, and two gas diodes that Mauchly had built previously, as we have seen.
In Atanasoff s hand are the words “J. V. Atanasoff’ and the initials “ISC†of Iowa State College and the phrase “$2 per’ digit.â€
As exhibited by the diagrams and notes on the paper, Mauchly freely discussed the possible components for an electronic digital computer. Atanasoff then said, as Mauchly later testified,
. . . that he had under construction at Iowa State College a digital computer of his own design whereby he hoped to do a great deal of computation, and rather quickly. But when I asked him for further information on this, he said that he would not reveal this in any detail whatsoever-that the only way more information on this could be obtained would be by a personal visit to his laboratory at Ames, and he invited me to make such a visit. In explanation of this position which he assumed with respect to giving information, he said there were complications which he had to take account of, and these complications seemed to arise from the fact that IBM or some other large company might be seeking knowledge with respect to his device. [Mauchly deposition, p. 313, Sperry Rand v. Control Data Corporation, Civil Action 15823]
Atanasoff was not trying to keep secret the fact that he was building a computer. He was just not revealing the method of operation, as evidenced by an article that appeared in the Des Moines Tribune on January 15, 1941, shortly after his meeting with Mauchly. The news release, entitled “Computing Device,†says:
An electrical computing machine, said here to operate more like a human brain than any other machine known to exist, is being built by Dr. John V. Atanasoff, Iowa State College Physics Professor. The machine will contain more than three hundred vacuum tubes and will be used to compute complicated algebraic equations. Dr. Atanasoff said it will occupy about as much space as a large office desk. The instrument will be entirely electrical and will be used in research experiments. Dr. Atanasoff said he had been working on the machine several years and probably will finish it in about a year. [Vol. 12, p. 1858, PX 670]
Atanasoff did not describe his “computing machine†to Mauchly beyond what is implied by this Tribune article, and he left Mauchly with the distinct impression that Atanasoff’s machine was all electronic. The phrase “$2 per digit†that Atanasoff had written on Mauchly’s notes made Mauchly very curious indeed.
Mauchly was stimulated by his meeting with Atanasoff. He had finally found someone who said he was trying to build a digital computer using vacuum tubes. His previous searches for a fast computing device had led him to investigate the multipliers being built by IBM and Remington Rand. The Remington Rand multiplier did a fast multiplication because it stored partial products (in mechanical cams), and this was the inspiration for the partial-products matrix that was built into the electronic multiplier of the ENIAC. Mauchly attended a meeting at Dartmouth College in the summer of 1940 and learned about George R. Stibitz’s relay calculator. (Mauchly believed that Stibitz was the first to call his device “digital.“) At Dartmouth, Mauchly met and talked with Norbert Wiener. They discussed computers and agreed that “electronics is the way to go,†but Wiener did not indicate that he himself had any plans for going in that direction.
Even though the scientific literature of the day described electronic circuits for binary counting (scaling circuits using pulses for counting), nothing described how to control these pulses for multiplication or division, or for storing digits for future use, as Mauchly was planning to do.
Mauchly was delighted to have found in Atanasoff a believer in electronic computing. Two men in different parts of the country, inspired by entirely different motives, had independently arrived at the idea that electronics could be used in a calculating device. Yet their goals were different, and their approaches were different.
Mauchly’s goal was to have a machine that would do the arithmetic of a conventional mechanical calculator, but it would use electronic tubes to do this arithmetic at electronic speeds, and do it automatically because it would have electronic switches for storing and retrieving the intermediate results. The results of the arithmetic would be available on separate registers within the machine for further processing. The machine would be general purpose, of course.
Atanasoff’s goal was to have a machine that would solve simultaneous linear algebraic equations in 29 unknowns using the method of Gaussian elimination. The evidence from the Honeywell trial reveals that Atanasoff first began the study of mechanizing these solutions in 1937 by designing a modification of an existing IBM tabulator, but the storage facilities were too small. He next turned to the idea of ganging together 29 conventional desk calculators in such a way that they would be synchronized in performing the necessary subtractions (divisions) for a mechanized solution to these equations.‘That was much too expensive, and he turned to the rotating-drum idea for storing and subtracting the coefficients of the unknowns. (At about this time, Irven Travis of the Moore School had independently explored the possibility of ganging together conventional desk calculators for the solutions of equations. The initial cost looked reasonable, but the wear and tear on the parts after a year or two of operation would affect the reliability and eventually the overall cost.)
Mauchly did not know that Atanasoff’s machine used a rotating drum and was essentially electromechanical, not electronic, so he was deeply puzzled as to how Atanasoff could build a machine for $2 per digit. The expense of electronic tubes was Mauchly’s greatest concern, not the job of connecting them. On January 19, 1941, Mauchly wrote to Atanasoff.
I am wondering how your plans with regard to computing devices are working out. Need I say that I await with some suspense the time when you will be able to let me have more information? How the recording end functions is the biggest puzzle, I guess. 450 digits at less than $2 per digit sounds next to impossible, and yet that is what I understood you to say, approximately.
Your suggestion about visiting Iowa seemed rather fantastic when first made, but the idea grows on me. I’ve gone so far as to note that our Spring Recess is March 21 to 31, whereas the meetings in Washington are about May 1. The financial problems involved in a long trip haven’t been solved, though.
If you aren’t too busy, perhaps you can drop a few hints as to your progress. [PX 675]
Atanasoff’s response to this letter on January 23, 1941, held out the carrot.
Just after my return we had a visit from Dr. S. [Samuel] H. Caldwell of MIT, who gave me a rather complete picture of calculating machine activities in the country. His visit gave me the urge to attempt the construction of a differential analyzer4 on a dime-store basis. I believe this attempt could be rather successful, and it is something I have laid away for future activity when my work gives out. By all means arrange to pay us a visit in Ames during your Spring Recess if this is possible. Our Spring Recess is from March 19 to 24, and I can think of many things that I would like to talk to you about. This list includes statistical Fourier analysis, resistance harmonic analyzers, computing machines of all kinds, and I suspect there are plenty of other things. I will be glad to have you as my guest while you are in Ames. As an additional inducement I will explain the two dollars per digit business.†[PX 676]
Mauchly replied to Atanasoff on February 24,194l.
Your invitation and promised explanation are indeed powerful inducements,and I hope that I shall be able to take advantage of them.
Somewhere-was it in Nature-1 saw an article on differential analyzers which included a picture of an analyzer constructed largely of Meccano parts [made by Douglas R. Hartree]. I think the “dime-store†analyzer ought to be successful. it did no more, it would justify If itself in merely aiding students to understand the process mechanical solution of differential equations. Incidentally, do you consider the d. analyzer an “analogue†machine?If so, how about a polar planimeter?
My crew of NYA people has been augmented,but perhaps not for the better. The new members are fit only for adding machine work, and even then can’t get the same total more than two out of three times (so it seems!).
Here’s hoping that you have made progressin Iowa, and that I’ll get out to see it all. [PX 699]
In anticipation of his visit to Ames during the spring break, and in hopes of getting the answer to the $2 per digit question, Mauchly spent every evening in his lab looking for a solution to this most perplexing problem: if Atanasoff is using vacuum tubes in his circuits, and each vacuum-tube assembly costs $2 or more, how can he possibly produce a computer, which must certainly contain devices for storage, arithmetic, and read-out, at that price? Furthermore, since vacuum tubes operate at such tremendous speeds, the switching needed for automatic operation would also require quite a few vacuum tubes. The answer must be that one vacuum tube was being used to represent many digits. So, starting January 1, 1941, Mauchly began exploring in his lab and in circuits on paper (produced at the Honeywell trial [PX 6651) various ways of getting more information with fewer vacuum tubes.
His experiments along this line were in the design of circuits that had a digit represented by the amount of current or the amount of voltage at various places. He also tried circuits in which the digit was represented by its position in a stream of 10 pulses. For example, the number 3 could be represented by one pulse occurring in the third position in a stream of 10 pulse times. (Today this would be called pulse-position coding.)
Mauchly also wrote to General Electric for information about various tubes, particularly about the possibility of GE building for him some gas diodes that would perform better by having a greater range between their ignition voltage and their sustaining voltage.
Mauchly’s plans for getting to Iowa during the spring break fell through. Meanwhile, he continued working out his computer and constructed a number of the decade counters for it. These were, of course, the biquinary counters using gas tubes; he was eager to get something built and working.
On April 26, 1941, Mauchly wrote to H. Helm Clayton. (Mauchly had borrowed a calculator from him for use in the weather-analysis project at Ursinus.)
As our work progresses, there will be more need for reducing long series of daily values to some standard form by multiplication or division. Hence we are still thinking about and working on electrical computing circuits, as I wrote in a previous letter. Some of the simple components of an electronic computer have been constructed, and we find they work, so we are going on to the real job of putting the components together …
In June I am thinking of doing two things. One is to go to Ames, Iowa, to see an electric computing machine being developed there in the Physics Dept. by a friend of mine, and the other is to further the construction of my own devices. [Mauchly Collection]
Mauchly continued his correspondence with Atanasoff. On May 27, 1941, he wrote:
Well, anyway there is more than a little prospect of my making a trip, starting from here about the tenth of June. I have a passenger who will very likely pay for the gas,and that will help.
From your letters I have gathered that your national defense work is unconnected with your computing machine. This puzzles me, for as I understand it, rapid computation devices are involved in N.D. [national defense]. In a recent talk with Travis, of the EE School at U. of Pa., I asked him about this, and the matter seemed same way to him. But if Caldwell has looked the over your plans (I think you said he was out there) and hasn’t seen any N.D. possibilities, I suppose that means your computer is not considered adaptable to fire control devices,or that they have something even better. Travis (who goes into active duty with Navy this week) pointed out the advantages of lightness and mass-production for electronic computing methods, but said that when he was consulting with General Electric over plans for the G.E. differential integraph [differential analyzer] they figured it would take over one-half million dollars to do the job electronically, and they would spend 1/5 that, so they built the mechanical type with Polaroid torque-amplifiers. It’s too bad you couldn’t stop when you were East-but try again-no doubt you will have to come East more often. [PX 789]
Atanaoff replied on May 31, 1941.
As you may surmise, I am somewhat out of the beaten track of computing machine gossip, and so I am always interested in any details you can give me. The figures on the electronic differential integraph seem absolutely startling. ‘During Dr. Caldwell’s last visit here, I suddenly obtained an idea as to how the computing machine which we are building here can be converted into an integraph. Its action would be analogous to numerical integration, and not like that of the Bush Integraph which is, of course, an analogus [sic] machine, and the steps in the numerical integration could be made arbitrarily small. It should therefore equal the Bush machine in speed6 and excel it in accuracy.
 Progress on the construction of this machine is excellent in spite of the amount of time that defense work is taking, and I am still in a high state of enthusiasm about its ultimate success. I hope to see you within two or three weeks. [PX 794]By this time Mauchly had made sketches of many different circuits for his decade counters and their control [PX 6651. Despite all efforts at economy, while preserving reliability, he could not design a decade counter assembly that would cost him less than $13 per decade. There was no way Mauchly could personally afford to construct many decades, and Ursinus had no funds for such research. He must find another way. Mauchly at this time was uncertain of his future at Ursinus because it was becoming increasingly hard for him and his family to live on his low salary. There seemed to be lots of opportunities opening up in defense industries, so he began looking for work in electronic computing and control devices. Just before he left to visit Atanasoff he sent a letter to George Bailey in the Office of Scientific Personnel, in which he stressed his interest in computing (June 7, 1941).
I have already filled out the Specialized Personnel check lists in Physics, Statistics, and Meteorology; in each of these I indicated my interest in electrical computing devices, and electronic devices particularly. … I don’t think I qualify as an “expert†in radio engineering, but my deep interest in electronic computing and control devices is accompanied by practical laboratory work, leading now to the construction of a high-speed electronic computing circuit. Incidentally, during the next week I am going to Ames, Iowa, to visit with Dr. Atanasoff of the Iowa State Physics Dept. and to discuss with him the pros and cons of his electronic computer versus mine. [ Mauchly Collection]
Visit to Atanasoff
The only way Mauchly could afford the trip to Iowa was by having riders who would pay for the gasoline. So he arranged to drive his next-door neighbors (a farmer named Jonas Schreffler and his elderly mother) to Freeport, Illinois. He also brought along his six-year-old son, Jimmy, whose only remembrance of the long trip from Pennsylvania to Iowa in a light car over very bumpy roads was, “We just drove and drove.†Mauchly arrived at Atanasoff’s house on Friday evening, June 13. That evening they discussed (as Atanasoff has testified) “such gossip as he could bring me of computing machines from the East.†The following morning Atanasoff took him to see the machine. Here at last was the answer to the intriguing “$2 per digit.†It was a shocker! I quote from Mauchly’s testimony at the Honeywell trial, but the idea is one I heard him mention many times before that.
It was a disappointment because there had been nothing said in my meeting with him at the University of Pennsylvania which indicated that this machine was not a fully electronic machine. That’s why my great curiosity, my great wonderment, how in the world did he do this for $2 a digit, because I was thinking in terms of all-electronic things, which make use of electronic speeds. Almost immediately, of course, when I got out there, I began to learn, even though the machine was not operative, for instance, on Saturday, you could see the drum idea and you could begin to put together the picture that this is a mechanical gadget which uses some electronic tubes in operation, but it’s still restricted in speed and was not what I was interested in from the point of view of electronic speed gadgets. The fact that it was also being built specifically to solve a special class of problems, rather than a general class, was quite obvious, of course, but that wasn’t the thing that really worried me because what I had been looking for were ways of getting high-speed electronic things without paying too much for them.
Sure, this was electronic in part, but it became perfectly clear without much examination or talking that it wasn’t electronic in whole, and it was sacrificing too much of the electrical end. So I think that a lot of the conversation that we had out there was really going over this point of “Why don’t you do this or why didn’t you do that?†His machine was specifically, deliberately constructed with the idea that when finished it would solve simultaneous linear algebraic equations, which is a very special class of problems.
But there are many other problems which cannot be handled in this way and my interest was in solving some problems which couldn’t be handled this way. And I could see that other people would be interested in solving still other problems which couldn’t be handled this way. So my general interest was in trying to get computers which would be versatile and not restricted to some one class of problems. [Vol. 77, p. 11,830]
Mauchly visited the machine with Atanasoff again on Monday, and this time Clifford Berry was there to demonstrate its operation. Atanasoff has described the machine at the time of Mauchly’s visit in June 1941.
I had asked Mr. Berry to get the machine in as complete as possible form while Dr. Mauchly was visiting. I remember the main shaft was off the machine when I spoke to Clifford Berry about it, so he assembled the parts. The base 10 “card in†device was on the machine while he [Mauchly] was there. The “base 2 in†and “base 2 out†units had temporary connections while he was there. They could be mounted on the machine to indicate the mechanical arrangements here, but they were not connected underneath. We had no ability to read from a base 2 punch card at that time. [Vol. 17, p. 2434]
The “timing-control contacts†device was not in place, nor had it been designed at this time. Instead, there was a manual switch that enabled the machine to cycle one cycle.
We still had to build a number of controls, such as controls for detecting the carry through. We had to build a plus-minus recognition unit for the drum so that we could tell whether it had a plus or minus number in it. [Vol. 17, p. 2432.]
The “boost and carry drum†was designed and built after Mauchly’s visit.
At the time of Mauchly’s visit, only one drum was mounted on the shaft. The card reader was not operative so numbers were put into the machine by placing them on the drum with a charged probe. Shifting was done by hand because control apparatus was not built. [Vol. 17]
When asked about multiplication and division, Atanasoff answered,
The thing that was missing on multiplication and division on this machine was the enumerator of the count [of each addition and subtraction] so there does not appear on the output of the machine, even if it were complete, the products and divisions [quotients]. [Vol. 18, pp. 2711-2712]
The ultimate goal of the ABC (Atanasoff-Berry Computer) was to solve 29 simultaneous algebraic linear equations with 29 unknowns. The machine never accomplished this goal. A set of just five equations with five unknowns would have required the intervention of the operator over 500 times to eliminate the unknowns. The amount of operator-intervention steps increased by the cube of the number of coefficients. In the case of five equations with five unknowns, 29 or 30 steps of operator intervention were required for one reduction into the next lower equation, or about 565 steps in the solution. It took about 17 minutes of running time to do the additions and subtractions and shifts for the five simultaneous equations, exclusive of the time for the operator to put in these 500-600 steps. The amount of time for the mechanical solution on the ABC was roughly equivalent to the amount of time required to get the solution by hand. This machine could not be described as automatic. Atanasoff said,
At Dr. Mauchly’s visit the machine was in no condition to carry out a full demonstration of these steps. Quite a number of the things necessary for these steps hadn’t even been worked out. Only the function was described to Dr. Mauchly, not the details of the structure. [Vol. 19]
In the ABC the drums containing the numbers revolved at the speed of one revolution per second. The revolving drums fed the binary digits of the coefficients serially into 30 separate adder assemblies, effectively restricting the speed of the unit to one addition time per second. Mauchly puzzled over this. Why was Atanasoff using expensive vacuum tubes in the add-subtract unit when the whole advantage of them-their speed-was lost completely by the slow-moving, gear-driven drum? On the other hand, since he had the funds to buy vacuum tubes, why hadn’t he designed electronic circuits for storing his digits instead of relying on a slow mechanical rotating drum? The capacitor drum had pulse rates so slow that Atanasoff could just as well have used relays instead of vacuum tubes in his adder. Relays would have been cheaper and more reliable than Atanasoff’s adder circuits; besides, they were already developed at the time. Atanasoff admitted that although he had thought about flip-flops, he had never been able to solve the stability problem. Atanasoff testified,
I have tried to place the time of my first knowledge of it [flip-flop] and it runs in my mind that scale of two circuits and flip-flops were used for scaling cosmic rays as early as 1933. I had never used one but I saw it in the literature. Flip-flops were made to work in cosmic rays in those days, but they were sensitive to the kind of pulses they got, and the form of the pulses. The few experiments I did, and they were few, made me unhappy about that direction of approach. [Vol. 16]
The whole issue of $2 per digit Mauchly to Iowa in the first place was no unimportant. It didn’t matter how much it tremendous speed and versatility offered were not being utilized. That morning Atanasoff gave Mauchly a copy of his manuscript to read, with strict admonitions against keeping the copy or making any notes about it. A very disillusioned Mauchly glanced briefly at the manuscript and got the distinct impression that it was a proposal written to solicit funds for construction of the computer. He noticed that it contained a list of problems that used systems of algebraic linear equations, an explanation of why Atanasoff had chosen a base-two number system, and a description of the machine itself, as envisioned in August 1940. Mauchly read the paper to find out how Atanasoff had worded his “sales pitch.†Although Atanasoff’s manuscript mentions automatic control circuits, none were described in the manuscript-nor were any designed, built, or described at the time of Mauchly’s visit [Vol. 17]. Atanasoff’s patent application also mentions automatic controls (crucial elements in an automatic device) but gives no description of them. Despite repeated requests by Iowa State College, Atanasoff never supplied any drawings of these controls, and consequently no patent application was ever filed [Vol. 17, p. 2452]. No automatic programming for the ABC was planned or thought of. In a letter to Dawn Henry [Vol. 19, pp. 2894-28981, Atanasoff said: “The concept of a machine that can be programmed for any (or almost any) conceivable process was not a part of our early ideas.†The mechanical revolving drum setup precluded any branching or selection of variables. The most interesting thing about Atanasoff’s computer, from Mauchly’s point of view, was the use of condensers as memory devices. Atanasoff described their problems and how he solved them.
The trouble with condensers that they are leaky is devices and having charged a condenser,it will not stay charged, and this was the troublesome element of the era and this commenced give me concern. I came to to the conclusion that I could use condensers a memory as element by jogging their memory at regular intervals with a mechanism. The signal (on the condenser)is sensed, reconstructed, and reinserted continually as the slow shaft revolves. [Vol. 12, p. 1733]
Mauchly thought that Atanasoff’s way of “jogging the memory†was ingenious. Since Mauchly himself had been planning to use condensers as the memory element in his flip-flops, he was quite interested in seeing how someone else solved the problems with them. On Monday afternoon, Mauchly gave a talk to a group from the physics, engineering, and statistical departments of Iowa State. He talked about his work in the statistical analysis of weather data and the devices he was building and had built, such as the harmonic analyzer, for speeding up this analysis. On Tuesday Mauchly visited A. E. Brandt, a member of the statistical department for which Iowa State College was famous. Later that day he received a letter saying he had been accepted in a government-sponsored electronics course at the Moore School. In anticipation of once again becoming a student, Mauchly left with his little son early Wednesday morning, picked up his elderly passengers en route, and arrived back at Ursinus College Thursday night, June 19. Atanasoff and Berry worked on their machine for another 15 months. When asked about the condition of the machine as of September 1942, Atanasoff replied,
The “reading†part did not have a satisfactory reliability-about 95 percent-but not high enough to make the machine operative. We could not use the machine,because only way the machine could be the made usable for solving systems of equations was to get that data out after you had filled the machine and reduced the order of equations by one; then you had to punch that card out and preserve it for future operation and then put it back in the machine. The machine did not have the internal memory necessary for carrying that information. That had to be punched out in the card. Since it wasn’t available, the complete function of the machine was not available.
The last thing I remember being done to test the machine [September 1942] was the elimination of one unknown between two equations. Now, these weren’t very long equations [each equation had 4 unknowns]. No system of equations was ever solved with this machine, but towards the latter part of the period before Mr. Berry left one day we placed the coefficients of one equation on drum fl, drum CA, and another equation on drum #2, KA, and one unknown was eliminated between them, after which it was punched out on a piece of paper. [Vol. 17, p. 2445.] Mauchly wrote to Atanasoff on June 22, 1941.
I drove to Southbridge, Mass. on Friday evening. On the way back East a lot of ideas came barging into my consciousness, I haven’t had time to sift them or but organize them. They were on the subject of computing devices,of course. If any look promising, you may hear more later. [PX 816]
He wrote to Clayton on June 28,194l.
Immediately after commencement here, I went out to Iowa State University [sic] to seethe computing device which a friend of mine is constructing there. His machine, now nearing completion, is electronic in operation, and will solve within a very few minutes any system of linear equations involving no more than thirty variables. It can be adapted to do the job of the Bush differential analyzer more rapidly than the Bush machine does, and it costs a lot less.
My own computing devices use a different principle, more likely to fit small computing jobs.
While at Iowa, I talked on the construction of harmonic analyzers. But I haven’t done anything about the 27-ordinate cost-estimate as yet.
All my time since coming back from Iowa has been taken up with an Emergency Defense Training Course at the Univ. of Pa. I had a chance to teach for the summer in a defense course given to high school graduates, but turned that down in order to become a student myself. I am working in electrical engineering and electronics. Whether or not I am given a defense job involving electronics later on, the training will be helpful in connection with electronic computing devices. [PX 822]
In analyzing the situation wrote in a diary note:
I thought his [Atanasoff’s] machine was very ingenious, but since it was in part mechanical, involving rotating commutators for switching, it was not by any means what I had in mind. [Vol. 82, p. 12,493]
Meeting J. Presper Eckert at the Moore School
Mauchly began the Emergency Science and Management Defense Training Course at the Moore School on June 23,194l. There he met J. Presper Eckert, Jr., a master’s degree candidate at the Moore School who was working for the summer as lab instructor for the government-sponsored course. Since Mauchly had already done most of the experiments with his own students at Ursinus, there was free time available to exchange ideas with Eckert. The youthful Eckert (12 years younger than Mauchly) immediately impressed Mauchly with both his tremendous knowledge of electronics and his open-mindedness about what was possible with electronics. Eckert already had a patent in the television field, on a light modulator using ultrasonic waves. Mauchly described to Eckert his ideas for building a computer using pulses from electronic tubes, to get some speed. Eckert had some experience in using pulses from vacuum tubes. He thought Mauchly’s idea was indeed feasible. Eckert’s attitude and design philosophy also appealed to Mauchly. Eckert determined what he wanted to do, considered what he had to do it with, studied the peculiarities of the components, and designed the apparatus in a most conservative manner, taking all the peculiarities into account. With this design philosophy, he thought he could build reliability, the most important characteristic of a computer, into the circuits. With encouragement from Eckert that it certainly was possible to build an all-electronic digital computer using the known technology, Mauchly analyzed and clarified his thinking in one of his frequent “diary notes,†quoted in full here. Mauchly attributes the terminology analog and impulse to Atanasoff, defines an analog device, and then declines to discuss analog any further. He gives all his attention to his real interest-an electronic digital “commercial competitor for the desk type mechanical computer.†The mechanical desk calculator is still the model for Mauchly’s computer; he is still thinking of a fast, cheap, flexible vacuum-tube computer such as he was working toward at Ursinus. He talks of having multiple registers for storing data and a separate unit for the arithmetic. His ideas for automatic control are still in the formative stage.
Notes on Electrical Calculating Devices
August l5, 1941Â JWM personal diary notes
1. Analog versus impulse types. Computing machines may be conveniently classified as either “analog†or “impulse†types.*
The analog devices utilize some sort of analogue or analogy, such as Ohm’s Law or the polar planimeter mechanism, to effect a solution of a given equation. The accuracy of such devices is obviously subject to limitations; at times the attainable is more than sufficient, but there is increasing need for more computational aid not so restricted. Impulse devices comprise all those which “count†or operate upon discrete units corresponding to the integers of some number system. There is no theoretical limit to the accuracy to which such devices will work; practical limitations on the bulk or cost or convenience of operation provide the only restrictions. The usual mechanical computing machine, utilizing gears, pauls, etc., are examples of impulse calculators.
* I am indebted to Dr. J. V. Atanasoff of Iowa State College for the classification and terminology here explained.
No further attention will be given to the analog type here for although differential analyzers and other analog machines are now being used and will continue to be used for some problems, it is in the impulse machines that major improvements in speed and accuracy are to be expected and sought for.
2. For speedy (and noiseless) operation, vacuum tubes and associated circuits are the obvious answer. There are no essential differences in designing vacuum tube apparatus to do the job of ordinary mechanical calculators … but after taking care of stability, freedom from error, ease of servicing, etc. one might conceivably wind up with design too costly to build. But economically feasible designs are possible. At present it may not be possible to build a commercial competitor for the mechanical desk computer, but larger machines for more involved, more lengthy, or more specialized jobs are practical. In some cases is possible to it materially decrease number of tubes and circuits the required in a large machine by having many similar operations performed by one and the same unit, which is switched around in sequence, rather than by having many duplicate units operating simultaneously. This is possible because the time required for a single elementary operation may be very short compared to the time allowable for completing one “step†in the calculation.
3. The basic units of any computing device are usually the following: A. Input registers, for putting in (storing) the numbers to be operated on. B. The adding (or add-subtract) mechanism for combining such numbers. C. The Output register for storing, indicating, or making a permanent record of the results obtained in units A and B.
There is usually some difference in the function or form of the various registers comprising A and C. For instance, in the ordinary mechanical computing machine, a keyboard may be used to put in a multiplicand, additional buttons of a different sort may be used to put in the multiplier (which determines the number of times a multiplicand is added to each of several carriage positions), and the resulting will be read off from dial registers. These dial registers do not make any permanent record, nor can a number in that register be used immediately (without special tricks) as a multiplicand or multiplier.
In a flexible computing machine, it would be very desirable to have all the registers in which numbers may be stored immediately usable as either type A or type C. One can imagine a computing control panel such as the following. [Figure 18 is redrawn from PX 847.]
When Mauchly was writing this paper, he had not yet resigned his position as head of the Physics Department of Ursinus College, nor did he yet have any indication that his application for a teaching job at the Moore School (made at the suggestion of Carl Chambers of the Moore School staff) would be accepted. Mauchly was actively seeking work in the electronics field, and he was also hoping for an increase in salary so that, if necessary, he could afford to build his “ideal†computing devices (keyboard types) according to the plans he had laid out in the preceding memo and in an earlier memo dated August 3, 1941. Mauchly’s requirements for his “ideal†computing device-general purpose, of course-were:
A. Considerable number of registers(add to these readily).
B. Ability to transfer numbers from one register to another at will.
C. Ability to operate with number in one register on other register without losing number in original register-so that it may be used again, or checked.
D. Provision for a certain number of constant factors in machine. (A + B), or preset switches.
E. Possible automatic sequence operations with of subtotals printed (for numerical integration). F. Ten-key operation? [PX 665]
All of these requirements ultimately appeared in the ENIAC except ten-key operation. On August 18, 1941, Mauchly wrote to his wife, Mary, in Collegeville to tell her of his employment situation. He says, in part:
Chambers told me that he told the Navy man that I should get at least $4000.Chambers wouldn’t take that to go himself, of course,for he figures that his job is actually worth 10,000to him.
I asked him what he thought I might be teaching the first year. “Nothing at all,†was his answer,“-at least hardly anything. You would probably have two hours a week of circuit theory, and two or three afternoons a week in the radio laboratory. That’s all, in the first year.â€
I haven’t had a chance to sound him out as to possibility of assurance promotion. I don’t believe on that, with the one-year probation, one could get any better arrangement than that if retained I would be advanced.
At any rate, their offer will be made within a week or so,thinks Chambers,for they want to get things settled too. Two things are now known: McIlwain is on leave, rather than resigning,and the man they hoped to get for one instructor has turned down the job. He is their A-1 graduate of last year, who has landed a full time fellowship at M.I.T., and being single, is quite able to turn down larger sums for the ultimate benefit of an M.I.T. degree.
Chambers also points out that under ordinary circumstances(McIlwain’s leave is not ordinary) no staff member at Moore School has ever been let go until he found another job. The school doesn’t restrict your publication in any way, and although it has rights to patents, it always releases engineering patents to the individuals anyway, so that’s that.
Philadelphia Electric had interviews but didn’t ask me around.
But the placement man-Sweeten-who now calls me by my first name-stopped me in the hall after my GE interview and said he wanted to see me soon to talk over another possibility. He thinks that I am just the man that Dr. Bush is looking for. [Mauchly Collection]
This letter indicates that there was an opening at the Moore School that Mauchly thought he would be asked to fill, and it gives us a brief view of what Mauchly believed to be the patent policy of the Moore School. When the Moore School offered him the position as instructor, starting in September, Mauchly accepted readily. He was still hoping to build a computer, but without a lab of his own to try out his various ideas, he began writing the thoughts about circuits that were occurring to him. In a group of papers of September 1941, entitled “Computing Circuits,†he explores a number of possible computing circuits.
1. JVA’s binary condenser system adapted to decimal system (like Stibitz’s use of relays for decimal calculation). 2. Scale-of-Ten Counting Device Two condenser circuits charged with ten equal pulses, one as reference, other has pulses“suppressed.†Output is the difference in the discharge time. 3. Frequency arithmetic Adding and subtracting frequencies having different frequencies for 10 digits. 4. Modify neon tube multivibrator delay circuits for counter computer use. 5. Add time delays (a) Sawtooth step wave with changing bias (b) Pulses going any one of (10) ways according to timing; each way in succession being open, others closed. [PX 869]
Other items referred to in these early notes indicate clearly that the basic units of computation that were ultimately used in the ENIAC had already taken shape in Mauchly’s mind: a multiplier, subtraction by complement, carry-over, a master pulser, and a pulse generator. We can see these reflected in the final ENIAC. Subtraction by complement was the method used for subtraction in the decade counters of the accumulators. The “master pulse? at this time was a pulse scheme between units for controlling the sequence of events. In later work with Eckert, the “master pulse? developed into the “master programmer†for initiating programs, for subroutines, and for branching. The “cycling unit†of the ENIAC was a linear descendant of Mauchly’s “pulse generator.†Mauchly describes this period.
Well, I was continuing to actively think about and talk to others about the possibility of using entirely electronic circuits to try to accomplish calculations, computing, for any kind of scientific or engineering job. [Vol. 77, p. 11,840]
Figure 19. Moore School faculty at the Mauchly farm near Ursinus College, probably fall 1941. Front row, left to right: Jimmy Mauchly, S. Reid Warren III, Alan Warren, Jimmy Chambers, Nancy Chambers. Middle row: Mary Mauchly, Sidney Mauchly, Marion Weygandt, Margaret Morgan (now Mrs. Joseph Matlack), Marian S. Warren, Mrs. Douglas W. Mode, Margaret M. Chambers, Carol P. Brainerd. Back row: John W. Mauchly, Arthur W. Burks, Cornelius N. Weygandt, Carl C. Chambers, Rachel (Mrs. S. J.) Mauchly, John Grist Brainerd, S. Reid Warren, Jr.
As a member of the faculty, Mauchly had an opportunity to look around and talk more freely with other faculty members. He invited them to a picnic at his farm in Collegeville, where his family were still living (Figure 19).
Mauchly wanted to talk about a computer, but there were few eager listeners. Irven Travis, who had been the one most interested in computing devices and had examined the possibility of building an electronic differential integraph for GE, had left for navy duty before Mauchly had come to the electronics course in June. With the single exception of Eckert, most of the faculty and staff of the Moore School doubted that electronics (on the large scale necessary) could be made reliable enough for digital computing.
Today, few will admit to having been doubters, but at the time they had good reason for their doubts. There was nothing new about the idea of using electronic tubes for counting pulses. Chambers had worked at Bartol Research Foundation and was familiar with the binary counters that had been built there for counting cosmic rays [Vol. 821. The flip-flop had been invented in 1919. The faculty knew that vacuum tubes were notoriously unreliable, and the idea of putting a thousand of them in a single device was naive, at best, and probably foolish. Their skepticism made Mauchly sense that they were not about to consider building his electronic computer.
Furthermore, the Moore School, like all U.S. educational institutions at that time, had limited funds for research. Its main computing instrument, the Bush Differential Analyzer, had been built in 1935 with government assistance to pay machinists and draftsmen. In a joint project with Aberdeen Proving Ground, the Moore School faculty had designed and built two analyzers-one for Aberdeen and one for the Moore School-based on the design of Bush’s MIT analyzer. While the Moore School did not have to assume the total financial burden, the initiative it displayed in getting a differential analyzer for itself showed that it was obviously interested in creating and having its own computing devices.
In the fall of 1941, there was plenty of evidence that war was coming soon and that the Moore School was already being involved. Not everyone shared Mauchly’s belief that fast calculating devices would be needed. In a private communication, Irven Travis has remarked that until the end of World War II, “for the then military applications, no further speed or accuracy than that of the Bush machine was needed. Ruggedness, manufacturability, and easy maintenance were important. Primitive forerunners of electronic computers were of little interest for National defence except in certain highly classified problems.†At that time the differential analyzer was the biggest computing machine in the world and was the fastest for some major problems. It was only in retrospect, when the electromechanical differential analyzer was compared with the ENIAC, that its speed and accuracy limitations were realized by its designers and users. Mauchly could see them then, however, because he could visualize the advantages of an all-electronic digital computer. Mauchly wondered if he could interest the Moore School in building a small machine that did the work of the differential analyzer-a digital electronic replacement-perhaps funded by the government as a possible wartime project.
Mauchly remembered that Atanasoff, in his May 31, 1941, letter had said he had gotten an idea, during Samuel H. Caldwell’s last visit, for converting his (Atanasoff’s) machine into an integraph. If Atanasoff had finished building the ABC, maybe he would be free to consider building the integraph. Mauchly had some good ideas that could improve Atanasoff’s machine in speed and ease of handling. One of these was certainly electronic switching instead of mechanical switching. On September 30, 1941, Mauchly, eager to get something built, wrote to Atanasoff proposing a joint venture.
As time goes on, I expect to get a first-hand knowledge of the operation of the differential analyzer-I have already spent a bit of time watching the process of setting up and operating the thing-and with this background I hope I can outdo the analyzer electronically.
A number of different ideas have come to me recently anent computing circuits-some of which are more or less hybrids, combining your methods with other things, and some of which are nothing like your machine. The question in mind is this: Is there any objection, from your point of view, to my building some sort of computer which incorporates some of the features of your machine? For the time being, of course, I shall be lucky to find time and material to do more than make exploratory tests of some of my different ideas, with the hope of getting something very speedy, not too costly, etc.
Ultimately, a second question might come up, of course, and that is, in the event that your present design were to hold the field against all challengers, and I got the Moore School interested in having something of the sort, would the way be open for us to build an “‘Atanasoff Calculator†(a la Bush Analyzer) here? [PX 870]
When asked about this letter at the Honeywell trial, Mauchly replied:
I was still, of course, very much interested in the problems of weather and the statistical ways of dealing with them, but I was looking closely at the differential analyzer and hoping that there would [be] a way of doing what the analyzer did (solving ordinary differential equations) with electronic computing circuits. [Vol. 77]
And when asked about the Atanasoff calculator, a la Bush Analyzer), he said:
In the previous correspondence somewhere Atanasoff had told me that he had some ideas for doing this. I didn’t know exactly what his ideas were. My contact with him indicated that he was a pretty intelligent fellow who had a lot of good ideas, and also that he wasn’t always saying everything he knew; that if he didn’t tell you exactly how he was going to do it, why, it didn’t mean he didn’t know. On the other hand, it didn’t mean that he was going to tell you if he did know. So this was a sort of an open proposition, that if you got something which you think might be useful to build, perhaps the Moore School could be interested in doing this. In other words, I was looking for any kind of project that would assist calculation. It looked to me as if Moore School was a good fertile field in which to get such things supported and, after all, they had built the differential analyzer. [Vol. 77]
Atanasoff’s reply to Mauchly’s letter came the next week, October 7, 1941:
I am delighted to hear that you are teaching in the Department of Electrical Engineering at the University of Pennsylvania, and I will be sure to get in touch with you the next time I come East which should be in the very near future. At that time we can discuss our mutual interest in calculators.
Our attorney has emphasized the need of being careful about the dissemination of information about our device until a patent application is filed. This should not require too long, and of course, I have no qualms about having informed you about our device, but it does require that we refrain from making public any details for the time being. It is, as a matter of fact, preventing me from making an invited address to the American Statistical Association. [PX 899]
This letter closed the door to any chance Mauchly had for working with Atanasoff at the Moore School, and also, as Mauchly understood it, to revealing or building any hybrid of Atanasoff’s design. Mauchly had already considered (on paper) a hybrid of Atanasoff’s idea of using condensers as a cheap storage. Now, not wishing to disclose any components of the ABC, Mauchly abandoned any schemes he had recently thought of for using condensers for storage and directed his thoughts to his original (at Ursinus) ideas that were “nothing like your machine†and used only electronic elements that were not limited in their computing action by mechanical parts.
Mauchly never found out until the time of the Honeywell case that although Atanasoff and Berry worked on their calculator for another year (until September 1942), they never finished it, nor did they ever file for the patents.
As often as he could, Mauchly discussed his computer ideas with Eckert. Eckert suggested that Mauchly bring in the ring counters and other components of his computer that were still in the Physics Lab at Ursinus. Eckert tested these gas-tube circuits on a bench at the Moore School. He concluded that although gas tubes were cheap and would work for this purpose, hard vacuum tubes offered the most promise. Vacuum tubes were much more flexible in circuit design and had the added advantage of greater speed. Eckert felt that a speed of 100,000 pulses per second was practical. The most important result of this testing was the boost it gave to Mauchly’s hopes. Eckert had convinced Mauchly that it was entirely possible to build a computer having only electronic elements. There was no reason why these elements could not be used in decade ring counters as Mauchly was proposing.
Mauchly packed up his biquinary ring counters, his pulse former, and his neon flip-flops and took them home. But on his desk throughout his years at the Moore School he kept one neon flip-flop, mounted in a coffee-container lid, blinking at him (see Figure 8).
The school year 1941-1942 was a busy one for Mauchly. In addition to his teaching (see Figure 20) (in two terms he had two junior classes, two senior classes, and a year-long evening graduate class), he was employed under government contract, making calculations of radiation patterns for radar work. He continued his discussions with Eckert, who encouraged him to think about ways to get outside funding. If it were peacetime, Mauchly would have approached the Weather Bureau, because his original thoughts had been on ways to compute the weather.
During this time GE intermittently used the differential analyzer in the basement of the Moore School for problems with which faculty members were associated. Cornelius Weygandt, of the Moore School staff, demonstrated to Mauchly how the analyzer solved differential equations. Mauchly began to expand his original ideas (based on the desk calculator) and started to determine how much equipment his computer would need so that it had the capacity to solve, by numerical integration, the same problems that the differential analyzer was now solving by analog. The proposed electronic machine clearly would have many advantages over the analyzer in speed, accuracy, and flexibility. Essentially, it could solve any problem that could be solved by a person using a desk calculator.
In July 1942, the Ballistic Research Laboratory (BRL) of Aberdeen Proving Ground, by agreement with the Moore School, took over the operation of the differential analyzer for the duration of the war. Joseph Chapline, a former student of Mauchly’s at Ursinus, was hired to keep the analyzer in running condition for the Aberdeen operators. BRL sent a nucleus of computing personnel, under the direction of John V. Holberton, from Aberdeen to Philadelphia. This group trained new employees (mostly women graduates with a degree in mathematics; I was one of them) in hand computing the trajectory of a missile using desk calculators. As the need for trajectories grew, the Moore School organized formal training programs to teach new employees without degrees the background mathematics needed to do the calculations.
Mauchly lost no time in acquainting himself with the ballistics equations, how they were solved by hand, and how the differential analyzer solved them. Here he saw an immediate use and need for his automatic electronic digital calculator and an agency that might support its development. He talked this over with Chambers, who had been somewhat sympathetic if not overwhelmingly enthusiastic about such a development. Chambers advised him to write a memorandum and give it to John Grist Brainerd, who was in charge of all government contract work for the Moore School. So Mauchly phrased his August 1942 memo in terms of what an electronic computer could do for BRL.
This memo, “The Use of High Speed Vacuum Tube Devices for Calculating†(see Mauchly 1942), sets down the advantages of an electronic computer over any mechanical or electromechanical device. He states very explicitly in this memo that the components he had planned are
. . . analogous to the ordinary mechanical computing machine. . . . It is intended that this analogy shall be interpreted mechanical rather completely. . . . Just as in a computing machine the digits which represent various powers of ten are added simultaneously,so in the electronic device. . . . It is in every sense electrical analogue of the mechanical the adding, multiplying and dividing machines which are now manufactured for ordinary arithmetic purposes. However, the design of the electronic computer allows easy interconnection of a number of simple component devices.. . . The result of one calculation is immediately available for further operation in any way which is dictated by the equations governing the problem.
Here was the point of departure from all other computer devices. Mauchly is offering the possibility of subroutines. Once again, Mauchly had set down his plans for an electronic computer, this time directed toward the mathematicians at BRL. The basic design is the same one he started with at Ursinus. It is also the same one that ended up in the ENIAC. The memo deals at length with the time required for various operations, probably as a result of his discussions with Eckert. It ends with a tailored sales approach-a comparison of the time required for electronic calculation of a trajectory with the time for the same calculation by hand with a desk calculator. Mauchly discussed this memo with Louis S. Dederick, civilian chief of mathematics at BRL. Dederick answered, according to Mauchly, “It would take at least a year to build a machine like this, and by that time, the war will be over†[Vol. 78]. When army lieutenant Herman H. Goldstine, who had been assigned as liaison officer to the Moore School in the fall of 1942, heard about the memo, he asked for a copy. None could be found. A new draft was made for Goldstine from the shorthand notes of Mauchly’s secretary. Two copies of this memo were introduced as evidence in the Honeywell trial. One was Goldstine’s [PX 12251. The other, which differed slightly in wording [PX 12271, was identified as having come from Brainerd’s file. On it was a note that read:
John: Read with interest. It is easily conceivable that labor shortage may justify development work on this in the not too far distant future. J.G.B.
Many writers of the history of the ENIAC have mentioned the seemingly peculiar disappearance of this memo. I recently discussed this with Eckert, who had a very reasonable explanation. He believes that Mauchly delivered the first typed copy of the memo to Brainerd’s secretary with instructions that copies be made on the school’s only mimeograph machine and distributed to the faculty. For whatever reason, the copies were never made, and the original, with the note on it, was filed in Brainerd’s filing cabinet, not to be seen again until almost two decades later.
Goldstine’s reaction to the memo was immediate and enthusiastic. He went through the proper channels and asked Brainerd for a proposal from the Moore School. Brainerd, Eckert, and Mauchly then prepared an outline of what such a proposal should contain. They divided the work so that Brainerd wrote the introduction and general parts of the proposal, and Eckert and Mauchly produced the technical parts. Mauchly sought Eckert’s aid in writing the technical parts, thus bringing Eckert formally into the project. Eckert (1954) discusses this point.
Then the Aberdeen people-I suppose that would be Col. Gillen, who was at the Pentagon, and several other people at Aberdeen-expressed interest in this, and it was at this point that I was brought into this matter. My connection with this matter previous to that had only been informal, that I had discussed these matters with Mauchly. At that time I was brought formally into the matter because background on pulse-circuit my techniques due to the radar work had at that point advanced to more than anyone else available.
The final proposal was presented to BRL in April 1943. Its title was “Report on an Electronic Diff.* Analyzer, submitted to the Ballistic Research Laboratory, Aberdeen Proving Ground, by the Moore School of Electrical Engineering, University of Pennsylvania.†The asterisk at Diff referred to a footnote explaining why the word was abbreviated [Vol. 80, p. 12,278]. It was in the introduction to the proposal that Brainerd, despite Mauchly’s objection, introduced the term Diff. Analyzer. Mauchly felt that the name should reflect the fact that the machine was to be general purpose and in no way limited to difference equations. Colonel Paul Gillen of the Aberdeen Proving Ground suggested the name ENIAC (Electronic Numerical Integrator and Computer), and this acronym was approved by Brainerd, Goldstine, Eckert, and Mauchly. The “and Computer†was to eliminate any misunderstanding about its origins. From the beginning, the ENIAC was intended to be a general-purpose machine, even though Aberdeen’s immediate use of it would be in the solution of ballistics equations. Even before the final contract was signed, the Moore School assembled a group of engineers, and work on the ENIAC began.
Epilogue
After my marriage to Mauchly in 1948, I resigned my job at Aberdeen Proving Ground and became a full-time wife and mother to a growing family (Figure 21). Eckert and Mauchly continued as a team and together designed the EDVAC, BINAC, and UNIVAC (Figure 22). Mauchly maintained his intense interest in the use of computers, and particularly in their use in solving problems of weather, for which he collected a houseful of data and several computers of his own. Figure 23 shows Mauchly in our living room shortly before his death on January 8,198O.
[Note: the following article was originally printed in IEEE Annals of the History of Computing, rx Vol. 6, ask No. 2., pilule April 1984.]
John Mauchly’s Early Years
by Kathleen R. Mauchly
The paper describes John W. Mauchly’s experiences and experiments that led to his concept of an electronic digital computer based on mechanical desk calculators during the years he was teaching at Ursinus College (1933- 1941), his interaction with John V. Atanasoff of Iowa State College, and the environment at the Moore School of Electrical Engineering at the University of Pennsylvania that led to the eventual proposal (1943) for building the electronic ENIAC.
Foreword
It is well known that many aspects of the ENIAC development are controversial, but it is the belief of the editors of the Annals that the publication of a variety of views of this development-by participants, observers, and scholars-will help clarify an important part of computing history. One of these views is given in the following narrative by John W. Mauchly’s widow. It reports the flavor of the times before the ENIAC and introduces some new information about Mauchly’s thinking and objectives.
A central feature of the ENIAC controversy is the 1971- 1973 Honeywell versus Sperry Rand litigation, which put much historical information into the public record. Kathleen R. Mauchly refers to this trial for some parts of her story and explains, in her preface, why some important details of her narrative were not put into evidence there. The reader should remember that litigation is an adversary procedure conducted by lawyers who are fundamentally concerned with winning their cases. Any contribution their efforts may make to the discovery of the truth is secondary to this basic aim. In court, witnesses are questioned to elicit answers that will support the questioners’ cases. Indeed, a frequent admonition to young trial lawyers is: “Never ask a question of a witness in court to which you do not know the answer. †A judge tries to arrive at a verdict according to the true facts as they apply to the law, but the judge can only do this in terms of the evidence presented in court by the contesting lawyers supplemented by questions from the bench. Consequently, while the evidence presented in the ENIAC litigation and the judge’s comments and decisions are important parts of the EN/AC history, they cannot be taken uncritically as the truth, the whole truth, and nothing but the truth about past events.
Several referees of this paper objected to the author’s interpretations of some of the events and circumstances described, and three of them have promised papers for the Annals that may take the form of narratives, other views, other interpretations, or specific comments and criticisms of this article. These will be considered for publication on the same basis as all other submissions.
It is not the policy of the Annals to seek or encourage controversy, but where the controversy exists (and the very existence of controversy is an important historical circumstance), the Annals will not shirk its duty to solicit and publish high-quality historical writings.
-Eric A. Weiss, Biographies Editor
Preface
The development of the ENIAC (Electronic Numerical Integrator and Computer) flows in a simple, logical, natural way from the work of John William Mauchly while he was at Ursinus College in Collegeville, Pennsylvania, and from the genius, inventiveness, and experience of his partner, J. Presper Eckert, Jr. Mauchly’s background and work prepared him for his part in the conception, design, and construction of the first electronic digital computer.
The material I present here is based partly on my own recollections of discussions with my husband, supported and extended by conversations with Eckert and by a study of depositions and testimony from various trials,’ of Mauchly’s own written articles, of tapes of his talks and videotapes of interviews (particularly an 18-hour videotape made by Esther (Mrs. John) Carr in 1977), of documents, letters, and scientific magazines of the 193Os, and of other artifacts that Mauchly saved during his lifetime. Much of the documentary material has already been deposited in the Van Pelt Library of the University of Pennsylvania (Mauchly Collection), where it is being cataloged and will be available for research purposes. Many of the items I discuss in this article are still in our home in Ambler, Pennsylvania, awaiting transport to the library. There are many places in a 21-room house and huge barn where one can store (and temporarily lose) boxes of papers and journals, old bills and receipts, and records.
After Mauchly’s death in 1980, while I was assembling the papers to be given to the Van Pelt Library, I came across a letter file from the Ursinus period. This box had been sealed for nearly 40 years, and its contents had not been known at the time of the 1973 Honeywell-Sperry trial in Minneapolis. In the file were carbons of letters showing that Mauchly had been actively working on a computer at Ursinus-something he had claimed all along.
Besides these paper items, we have the physical components of the electronic computer that Mauchly was building during the time he was teaching at Ursinus College. These components alone are evidence that Mauchly’s concept of an electronic “computer-calculator†predated any association with John V. Atanasoff and led directly to the design of the ENIAC.
Reviewers of an early draft of this paper have asked why this material was not presented at the Honeywell trial in which the presiding judge, Earl R. Larson, said, in part (seethe appendix to this article for further findings):
Eckert and Mauchly did not themselves first invent the automatic electronic digital computer, but instead derived that subject matter from one Dr. John Vincent Atanasoff, (Larson 1974, p. 47, 3.1.2)
The Honeywell-Sperry trial was in two parts. Sperry was suing to collect royalties, charging infringement of the ENIAC patent. Honeywell wished to avoid paying royalties by claiming that the ENIAC patent was invalid because of prior art (among other things) and charging Sperry with restraint of trade. The attorneys for Sperry may have been thrown off guard by the opening statement by Honeywell’s attorney, Henry Halladay:
The plaintiff’s case,your honor, does not deny that the ENIAC machine was a pioneering effort. Indeed some of the witnesses whom the plaintiff intends to call to testify will so say, that it was the premier machine, that it was a breakthrough. Indeed, we and Honeywell do not deny that the ENIAC machine, the ENIAC system, may well be considered a pioneering invention. [Vol. 77, p. 11,723]
The attorneys for Sperry had concluded, after hearing the testimony presented by Honeywell, that no evidence had been introduced to show prior art by Atanasoff or anyone else. H. Francis DeLone, attorney for Sperry Rand, said in his opening statement:
Beyond offering this massive collection of patents [218 in all] we do not see that Honeywell has tendered any evidence on the basis of which to assert a claim that the 606 [ENIAC] patent is invalid because of prior art, and therefore we do not contemplate in the presentation of our case offering evidence on that score because we do not think there is anything to meet with reference to these patents which have simply been put into the record, but to which there has been no testimony or explanation.
The statement by DeLone represented the thinking of the defense team.’ They had made a thorough search in the U.S. Patent Department and found that Atanasoff had never applied for or been granted any patent on any computing device or part of a computing device. The evidence presented by the plaintiff had proved to them that Atanasoff never had a working device. Furthermore, there had been no evidence that any of the 148 claims of the ENIAC patent read on Atanasoff’s work. With this thinking, unfortunate as it seems by hindsight, the Sperry team presented its case.
Mauchly and Eckert were not themselves parties to the suit. Since they were only witnesses, they had no control over the selection of counsel or the manner in which the defense would be conducted. Mauchly had repeatedly stressed to the Sperry lawyers the importance of bringing in some witnesses from the Ursinus period, but they disregarded any such suggestions. Consequently, although pictures of nearly all the devices Mauchly had built at Ursinus were introduced, and Mauchly described them for the court, no testimony was given to relate these devices to the ENIAC that was built later at the Moore School. The devices themselves were never brought into the courtroom and, of course, were never demonstrated.
Much of the material presented in this paper is documented in the Honeywell-Sperry trial exhibits. The material is important to understanding the history of ideas in computing and will contribute to an understanding of John Mauchly’s position in the history of computing.
My story starts with Mauchly’s high-school days and ends with the preparation of the proposal for funding of the ENIAC and the selection of its name. It touches on later events, particularly the Honeywell-Sperry trial, only as they give information about the period of my narrative.
My Part in the Story
My involvement with computers began in July 1942 where, shortly after receiving my bachelor’s degree in mathematics from Chestnut Hill College in Philadelphia, I was hired as a “computer†by the Ballistic Research Laboratory of Aberdeen Proving Ground. I was immediately sent to join the Ballistics Computing Group that had arrived at the beginning of that month at the Moore School of Electrical Engineering of the University of Pennsylvania. After learning how to calculate a trajectory by numerical methods using a desk calculator, I was assigned to operate the Moore School differential analyzer, and that was my principal assignment for the duration of the war.
In the spring of 1945, I was one of five women assigned to be programmer-operators for the ENIAC project, which was nearing conclusion at the Moore School. The manuals that would describe the ENIAC and its operation had not yet been written, and we did not have access to the parts of ENIAC that were being assembled, so we had to learn how the ENIAC worked by talking to the engineers and studying the block and timing diagrams.
The ENIAC was moved to Aberdeen, Maryland, in December 1946 and I continued my work with it in Aberdeen until I married John Mauchly in 1948 (see Figures 1 and 2).Â
Mauchly’s Work Begins
Mauchly’s interest in calculating and machines for calculating reached back to his childhood days (see Figure 3). As a high-school student he spent many hours after school and on weekends doing calculations for his father, S. J. Mauchly (Ph.D., Physics, University of Cincinnati), who was chief of the section of Terrestrial Electricity and Magnetism at Carnegie Institution of Washington. S. J. Mauchly developed the equipment and methods for observing and recording the electrical field strength of the atmosphere over land and over oceans. John became familiar with all the measuring instruments and calculating devices in his father’s office, even taking them apart for closer scrutiny. The calculations were done on a “Millionaire†calculator, an early machine that multiplied directly by collecting the units and tens digits of the partial products. Helping his father in the analysis of data sparked the young Mauchly’s interest in weather data and computation in general.
John Mauchly entered Johns Hopkins University in 1925 as an electrical engineering student, and after two years he transferred to the physics graduate school. His work both as a Ph.D. candidate and later as a research assistant at the Johns Hopkins Physics Laboratory (see Figure 4) involved long hours in the analysis of the spectra of molecules and the calculation of their energy levels. During the summers he worked in measurements and computation at the wind tunnel of the Bureau of Standards, where his boss was Hugh Dryden, who later became deputy chief of the National Aeronautics and Space Administration (NASA).
In 1933 Mauchly accepted a position as professor of physics at Ursinus College in Collegeville near Philadelphia, where he stayed until June, 1941. He felt he would like to continue his father’s work in atmospheric electricity, and he began to apply some new statistical techniques to the large body of geophysical data, which was growing ~year by year. Scientists at that time knew that solar activity affected the earth’s magnetic field, but most of them discounted the idea that solar activity could affect the weather. Mauchly set out to show, by statistical analysis of the geophysical data, and particularly meteorological data, that a relationship between the sun’s activity and the earth’s weather did exist.
With the help of some of his physics students, he collected surplus weather maps and other meteorological data from the Carnegie Institution, where he worked as a physicist during the summers of 1936, 1937, and 1938. He and his students also hand copied data from the vast storehouse of the U.S. Weather Bureau on M Street in Washington, D.C. Thanks to a government program, NYA (National Youth Administration), Mauchly was able to put about 12 students to work reducing these data. For this work he had several Marchant calculators and eventually one fully automatic Monroe.

Figure 5. Remains of an early attempt at a flip-flop counter using neon tubes, built around 1936. (Author’s collection)
The work was slow and tedious, and Mauchly began searching for ways to speed it up. He observed two things about hand computation that started him on the path for better, faster ways: (1) the labor one does in using a desk calculator is mainly in the entry of numbers in the keyboard, and (2) any errors made are usually the result of transcribing numbers incorrectly from the dials to paper, or from paper to the keyboard. Therefore, Mauchly’s first objective was to devise some equipment that would store any numbers once they had been entered on the keyboard a single time, so that they could be used as often as desired thereafter, rather than having to be reentered every time one wanted to use them. The equipment would have to perform the arithmetic-the additions, multiplications, etc.-in order to make use of the stored numbers. The original idea was a desk calculator with storage facilities. Through his association with Benjamin D. Wood, the statistician at Columbia University, Mauchly learned of the work in scientific computation being done there by Wallace J. Eckert. Eckert’s computations were made on plugged-together IBM machines. Mauchly investigated this setup, although he knew that IBM machines were too expensive for his limited budget at Ursinus.
Scaling Circuits
Mauchly was a dedicated teacher and made it a policy to take his best students to see the exciting things that he had seen in the nuclear physics research labs where former Hopkins classmates as well as some of his father’s colleagues were working. In the High Voltage Laboratory of Carnegie Institution, Larry Hafstad, Merle Tuve, and Gregory Breit had wired up some electronic tubes and built “scaling circuits†to count the pulses of an atom going through a gas. Their circuits were based on the Eccles and Jordan (1919) and Wynn-Williams (1932) work.
At the Bartol Research Foundation of the Franklin Institute of Philadelphia, W. F. G. Swann, a family friend and physicist from Carnegie Institution, had also built vacuum-tube scaling circuits for cosmic-ray work. These visits are recalled in a September 1,1982, letter to me from one of Mauchly’s former physics students, John DeWire, who has just retired from the Laboratory of Nuclear Studies at Cornell.
During the period 1936-1938 I visited both the Bartol Foundation and DTM [Department of Terrestrial Magnetism] with John, certainly several times in the case of DTM. We saw counting devices being used in both laboratories. At Ursinus we had a Geiger counter and some type of counting circuit, perhaps the equipment you still have. In my senior year I took a course from John, in which he used the text Atomic Physics by members of the physics staff at Pitt. In that text there are descriptions of coincidence circuits and other counting devices.
What I remember most clearly was John’s interest in flip-flops. I only did a little work on one, but quite a lot of work was done by another student whose identity I do not recall. All of us around John were fully aware that the motivation behind this work was to develop a device to do arithmetic calculations electronically using binary digits. John had many calculations under way and he was obsessed with finding ways to make these calculations less painful. One of my jobs was to solve some high-order simultaneous equations using a method called Synthetic Division. I spent many hours at an old Marchant doing this work and fully appreciated John’s interest in finding a better way to do the job.
In all these cases, vacuum-tube circuits were being used to “scale down†the rapid counts of more than 100,000 per second. A single switching circuit would give one count for every two counts put into it. The pulses from several of these circuits arranged in series would be fed into a mechanical counter. Mauchly began to think of ways he could utilize such a circuit. He reasoned that if one could generate pulses in his own way, then one could, with proper controls, use vacuum tubes to do arithmetic. All of the foregoing contributed to Mauchly’s thoughts about electronic computing. The year was 1936.
Learning the Electronic Arts
The scientific publications of the years 1936-1937, particularly Physical Review, Review of Scientific Instruments, and Journal of the Franklin Institute, were for Mauchly valuable sources for circuits for counting. The magazine Electronics was rich in points of technique and often provided more basic information than the physics journals. These publications illustrated the various types of ring counters that were being built using vacuum tubes. Mauchly felt that he needed to know more electronics to develop the control circuits, however, and in the fall of 1936 he enrolled in the evening graduate course in electronics at the Moore School of the University of Pennsylvania. The course, taught by Knox McIlwain, was directed to electronic theory rather than practice, so Mauchly fell back on the literature of the day and his own experiments for the control circuits.
Control Switches

Figure 8. Neon flipflop (with rectifier supply) from Mauchly’s desk at the Moore School. This was a demonstration model and was the one exhibited at the trial.
The computer he envisioned had decade counters controlled by electronic switches for the transfer of data from one counter or storage element to another. He first attacked the problem of electronic switching, the control of one set of signals by another. Because he couldn’t afford the cost of vacuum tubes for these experiments, he substituted neon bulbs. Although neon bulbs are not functionally interchangeable with vacuum tubes, the logic was the same. The neon bulbs worked electronically, and they gave a visible indication. They were slow compared with vacuum tubes, which the cosmic-ray scientists were using, operating at only a few hundred pulses per second, but they were cheap-a good tradeoff.
At first Mauchly got his neon bulbs by breaking open fuses and taking out the indicator capsules. Then he found he could buy these neons directly from General Electric for $8.00 per 100. With these neons he built his control devices. He wired up two neon bulbs with three resistors and one capacitor (condenser) and created, by interrupting the current through the circuit, the off-on action of a switch-one of the elements he needed for a computer. This device with one input that would throw it into an alternate state is called a binary counter; with two inputs the device is a flip-flop. He connected 10 of these simple neon-tube flip-flops in a ring and built for himself a trial decade counter (see Figures 5, 6, 7, 8).
Cipher Machine
Mauchly’s next use of these neons was in a cryptographic device he built and demonstrated to William Friedman at the Army Security Agency in Arlington, Virginia, in 1937. This device (1) was digital, using a base-3 number system; (2) utilized the flip-flop-the indicator lamps were either off or on; and (3) had a function table of nonlinear elements.
Mauchly had a lifelong interest in cryptography and built this device to illustrate some of his ideas. It contained equipment to encrypt and decipher and used a substitution method, employing a series of cards with different letters of the alphabet written in random order. A card would be placed so that the punched holes fell around the neon indicator lamps. The mechanical switches on the face of the device rearranged the wiring underneath. Mauchly would have preferred a standard keyboard instead of these switches, but none was available at the secondhand radio store where he usually~bought his equipment.
Each switch had nine positions, which, coupled with a smaller switch of three positions, gave the 27 positions needed for the letters of the alphabet and a space (Figure 9). Behind each switch was a cipher-changing switch. This was a band switch made up of a stack of wafer switches. Three letters at a time were fed into the band switches from the alphabet switches on the front, coded, and read into the corresponding neon tubes (Figure 10). This specialized device could be further described as a function table of nonlinear elements. With a few input signals, one could select as many as 81 possibilities.
The Decade Counter
About this time (1937) RCA brought out what Mauchly described as a “trigger tube,†a gas relay tube that required only a small signal to activate something that required a much heavier current. Mauchly bought many of these OA4G tubes and began experimenting with circuits that would advance in response to pulses the same way the ENIAC ultimately advanced to pulses using vacuum tubes. On a board with six sockets, he mounted five of these gas tubes connected in a ring, which, combined with a binary counter in the sixth socket, produced a biquinary device that could count to 10 (Figures 11 and 12). This counter did not require much electrical power and generated very little heat because only one tube out of five would be carrying current at any one time.
These cold cathode gas counters were satisfactory in that they showed Mauchly at that time the possibility for building a small, cheap electronic computer for his own use at Ursinus, even though the speed would be inferior to what could be expected from vacuum-tube counters or scaling circuits described in the literature or in use in the nuclear laboratories that he had visited.
The Pulse Former
A counter is of no use unless it is reliable, so to ensure reliability of the ring counters, some reshaping of the pulses going into the counter was needed. Mauchly built what he called a “pulse former,†similar to what was later used in the ENIAC, to precede the counter. He needed to know what kind of pulses were going into the circuits and what was happening to them in the circuits. The pulse former (Figure 13) reshaped the pulses that entered the counters. It was built on the same kind of pressed board as all the other components and contained a choke, an 884 gas tube, and a 6J7G (G stands for glass) power tube with screen grid. Simple manual switches regulated the height, width, and duration of the pulses. The pulses entering the pulse former were generated by a low-frequency oscillator. A small 3-inch oscilloscope from Culpman and Romander monitored the pulses for frequency and reliability. Mauchly was able to make the gas-tube counters, with the reshaped pulses, operate reliably at 500 pulses per second.

Figure 11. Biquinary counter circuit board showing six tube sockets (OA4G) and six clip terminals (five for digit tubes and one for a flip-flop to send pulses around a second time).
In 1939, the Moore School offered a course called “Theory and Design of Computing Instruments†to be given by Irven Travis. Mauchly signed up for the course, but it was canceled because there were too few registrants. He did meet Travis, however, and learned about the Moore School’s differential analyzer and about the advances, mostly electromechanical, that were being made in computing instruments at that time. Many of these were analog, such as the large network computers being designed by General Electric, Westinghouse, and Bell Telephone Laboratories.
The Harmonic Analyzer
While the experimentation in switching circuits and gas-tube counters was going on in Mauchly’s lab at Ursinus, the statistical analysis of geophysical and weather data continued, but at the slow pace of hand calculation and desk adding machines. To speed up this work, he built another computing device-a harmonic analyzer (Figures 14 and 15).
The accuracy requirements of the data were not great, so in this case an analog machine would do an adequate job of analyzing the data into waves. In the harmonic analyzer he built, all data were entered by setting knobs, and the read-out came on a high-quality meter that could read microamps. Computing was done by a series of circuits that responded to voltages changed by changing the settings on the dials. Under each knob was a General Radio potentiometer that was accurate to 1 percent. The device had a plugboard (banana plugs) to change the scale of the readings on the meter dial.
Regulating Power Supply

Figure 12. Back wiring of biquinary circuit. There are a number of these counter circuit boards, dating from 1939 to 1941, all showing different back wiring.
Because the accuracy of the harmonic analyzer depended on a reliable voltage input, it was necessary to build a device to ensure this reliability. The house voltage at Ursinus College varied as much as 15 percent, sometimes just because the freight elevator was in use. So Mauchly built a regulating power supply of an amperite tube and a group of other neon and argon tubes (Figures 16 and 17). With this he brought the voltage variation to within 0.5 percent, low enough to give him an overall accuracy of 1 percent.
The parts for these devices were bought from shops selling surplus or secondhand electronic ‘supplies. All of the devices are still in our home in Ambler, and they all still work.
With the harmonic analyzer, the speed of reducing the weather data improved considerably, and Mauchly was able to accumulate sufficient data to show a 27-day and a 13-1/2-day wave in the rainfall variations over the United States. Mauchly presented his results at a AAAS meeting in Philadelphia in December 1940; it was at this meeting that Mauchly met John V. Atanasoff for the first time.
Planning to Build

Figure 13. Pulse former (built 1937-1938) with switches to regulate height, width, and duration of pulses. An oscilloscope, not shown, was necessary for operation.
Before November 1940, Mauchly had successfully tested certain components of his proposed computer and convinced himself that it was possible to build a cheap, reliable digital device using only electronic elements. He was now ready to build. The machine was intended primarily for use in his own laboratory and would be paid for out of his own pocket. His students at Ursinus well remember his scrounging for tubes and other components that would produce a machine “with no moving parts.â€
He mentioned his intentions in two letters written in the fall of 1940. On November 15, he wrote a letter to H. Helm Clayton, a meteorologist with whom he had worked the previous summer, that was published in the Annals (Volume 4, Number 3, July 1982, pp. 247-248). One paragraph bears repeating.
In a week or two my academic work will not be quite so heavy, and I shall begin to give sometime to the construction of computing devices. We have further simplified the design of our proposed27-ordinate analyser. In addition, we are now considering the construction of an electrical computing machine to obtain sums of squares and cross-products as rapidly as the numbers can be punched into the machine. The machine would perform its operations in about l/200 second, using vacuum tube relays†and yielding mathematically exact, not approximate, results. That is, its accuracy would not be limited to the accuracy with which one can read a meter scale, but could be carried to any number of places if one cared to construct the machine with that many parts. With conventional tubes, it would be rather bulky, but special tubes could be designed to make it very compact. [Mauchly Collection] [Emphasis here and throughout is my own.]
It is plain that Mauchly was planning a digital device. On December 4,1940, Mauchly wrote to John de Wire.
For your own private information, I expect to have, in a year or so, when I can get the stuff and put it together, an electronic computing machine, which will have the answer as fast as the buttons can be depressed. The secret lies in “scaling circuits, †of course. [Mauchly Collection]
Here we have the seeds of an ENIAC: (1) ring (in this case biquinary) counters that could perform the arithmetic and store the numbers; these were the basic building blocks; (2) additional vacuum tubes for control and circuit switching so that the contents of the counters could be transferred from one register to another; (3) pulse formers with controls on amplitude and duration to precede each ring-counter circuit; (4) a low-frequency oscillator-type source for pulses. He planned a keyboard input for the data and operations. The design was based on the standard mechanical desk calculator, with electronic ring counters taking the place of the mechanical counters.
In his careful, methodical way, Mauchly had thought out, built, and tested the components of an automatic electronic general-purpose calculator. It had no moving parts. He used cold cathode gas tubes instead of vacuum tubes in his circuits because he thought that gas tubes would require less wiring and less cooling, and also he could see what was going on in the circuit. The use of gas tubes reduced the speed of operation well below what the current literature said was possible with vacuum tubes. The logic was the same, however, and the speed of l/200 second per operation would be quite an improvement over any then-existing machine.
Atanasoff
Mauchly first met Atanasoff at the AAAS meeting at the University of Pennsylvania on December 28,194O. Mauchly presented a paper on weather prediction and analysis and mentioned that the results had been computed on the harmonic analyzer he had designed and built. After the talk Atanasoff approached Mauchly, introduced himself, and mentioned that he, too, was designing and building a computer [Vol. 131. They briefly discussed harmonic analyzers and the possibilities of an electronic computer. In all, the conversation lasted less than 20 minutes.
The tangible evidence of that meeting are the notes on the back of Mauchly’s program [PX 22,420]. These notes, in Mauchly’s handwriting, indicate a discussion of the harmonic analyzer and the process of Fourier analysis, and they indicate that Mauchly discussed with Atanasoff the binary counter and/or storage circuit that uses two gas diodes as its nonlinear elements. In Mauchly’s hand is a circuit diagram of a binary counter containing three resistors, one condenser, and two gas diodes that Mauchly had built previously, as we have seen.
In Atanasoff s hand are the words “J. V. Atanasoff’ and the initials “ISC†of Iowa State College and the phrase “$2 per’ digit.â€
As exhibited by the diagrams and notes on the paper, Mauchly freely discussed the possible components for an electronic digital computer. Atanasoff then said, as Mauchly later testified,
. . . that he had under construction at Iowa State College a digital computer of his own design whereby he hoped to do a great deal of computation, and rather quickly. But when I asked him for further information on this, he said that he would not reveal this in any detail whatsoever-that the only way more information on this could be obtained would be by a personal visit to his laboratory at Ames, and he invited me to make such a visit. In explanation of this position which he assumed with respect to giving information, he said there were complications which he had to take account of, and these complications seemed to arise from the fact that IBM or some other large company might be seeking knowledge with respect to his device. [Mauchly deposition, p. 313, Sperry Rand v. Control Data Corporation, Civil Action 15823]
Atanasoff was not trying to keep secret the fact that he was building a computer. He was just not revealing the method of operation, as evidenced by an article that appeared in the Des Moines Tribune on January 15, 1941, shortly after his meeting with Mauchly. The news release, entitled “Computing Device,†says:
An electrical computing machine, said here to operate more like a human brain than any other machine known to exist, is being built by Dr. John V. Atanasoff, Iowa State College Physics Professor. The machine will contain more than three hundred vacuum tubes and will be used to compute complicated algebraic equations. Dr. Atanasoff said it will occupy about as much space as a large office desk. The instrument will be entirely electrical and will be used in research experiments. Dr. Atanasoff said he had been working on the machine several years and probably will finish it in about a year. [Vol. 12, p. 1858, PX 670]
Atanasoff did not describe his “computing machine†to Mauchly beyond what is implied by this Tribune article, and he left Mauchly with the distinct impression that Atanasoff’s machine was all electronic. The phrase “$2 per digit†that Atanasoff had written on Mauchly’s notes made Mauchly very curious indeed.
Mauchly was stimulated by his meeting with Atanasoff. He had finally found someone who said he was trying to build a digital computer using vacuum tubes. His previous searches for a fast computing device had led him to investigate the multipliers being built by IBM and Remington Rand. The Remington Rand multiplier did a fast multiplication because it stored partial products (in mechanical cams), and this was the inspiration for the partial-products matrix that was built into the electronic multiplier of the ENIAC. Mauchly attended a meeting at Dartmouth College in the summer of 1940 and learned about George R. Stibitz’s relay calculator. (Mauchly believed that Stibitz was the first to call his device “digital.“) At Dartmouth, Mauchly met and talked with Norbert Wiener. They discussed computers and agreed that “electronics is the way to go,†but Wiener did not indicate that he himself had any plans for going in that direction.
Even though the scientific literature of the day described electronic circuits for binary counting (scaling circuits using pulses for counting), nothing described how to control these pulses for multiplication or division, or for storing digits for future use, as Mauchly was planning to do.
Mauchly was delighted to have found in Atanasoff a believer in electronic computing. Two men in different parts of the country, inspired by entirely different motives, had independently arrived at the idea that electronics could be used in a calculating device. Yet their goals were different, and their approaches were different.
Mauchly’s goal was to have a machine that would do the arithmetic of a conventional mechanical calculator, but it would use electronic tubes to do this arithmetic at electronic speeds, and do it automatically because it would have electronic switches for storing and retrieving the intermediate results. The results of the arithmetic would be available on separate registers within the machine for further processing. The machine would be general purpose, of course.
Atanasoff’s goal was to have a machine that would solve simultaneous linear algebraic equations in 29 unknowns using the method of Gaussian elimination. The evidence from the Honeywell trial reveals that Atanasoff first began the study of mechanizing these solutions in 1937 by designing a modification of an existing IBM tabulator, but the storage facilities were too small. He next turned to the idea of ganging together 29 conventional desk calculators in such a way that they would be synchronized in performing the necessary subtractions (divisions) for a mechanized solution to these equations.‘That was much too expensive, and he turned to the rotating-drum idea for storing and subtracting the coefficients of the unknowns. (At about this time, Irven Travis of the Moore School had independently explored the possibility of ganging together conventional desk calculators for the solutions of equations. The initial cost looked reasonable, but the wear and tear on the parts after a year or two of operation would affect the reliability and eventually the overall cost.)
Mauchly did not know that Atanasoff’s machine used a rotating drum and was essentially electromechanical, not electronic, so he was deeply puzzled as to how Atanasoff could build a machine for $2 per digit. The expense of electronic tubes was Mauchly’s greatest concern, not the job of connecting them. On January 19, 1941, Mauchly wrote to Atanasoff.
I am wondering how your plans with regard to computing devices are working out. Need I say that I await with some suspense the time when you will be able to let me have more information? How the recording end functions is the biggest puzzle, I guess. 450 digits at less than $2 per digit sounds next to impossible, and yet that is what I understood you to say, approximately.
Your suggestion about visiting Iowa seemed rather fantastic when first made, but the idea grows on me. I’ve gone so far as to note that our Spring Recess is March 21 to 31, whereas the meetings in Washington are about May 1. The financial problems involved in a long trip haven’t been solved, though.
If you aren’t too busy, perhaps you can drop a few hints as to your progress. [PX 675]
Atanasoff’s response to this letter on January 23, 1941, held out the carrot.
Just after my return we had a visit from Dr. S. [Samuel] H. Caldwell of MIT, who gave me a rather complete picture of calculating machine activities in the country. His visit gave me the urge to attempt the construction of a differential analyzer4 on a dime-store basis. I believe this attempt could be rather successful, and it is something I have laid away for future activity when my work gives out. By all means arrange to pay us a visit in Ames during your Spring Recess if this is possible. Our Spring Recess is from March 19 to 24, and I can think of many things that I would like to talk to you about. This list includes statistical Fourier analysis, resistance harmonic analyzers, computing machines of all kinds, and I suspect there are plenty of other things. I will be glad to have you as my guest while you are in Ames. As an additional inducement I will explain the two dollars per digit business.†[PX 676]
Mauchly replied to Atanasoff on February 24,194l.
Your invitation and promised explanation are indeed powerful inducements,and I hope that I shall be able to take advantage of them.
Somewhere-was it in Nature-1 saw an article on differential analyzers which included a picture of an analyzer constructed largely of Meccano parts [made by Douglas R. Hartree]. I think the “dime-store†analyzer ought to be successful. it did no more, it would justify If itself in merely aiding students to understand the process mechanical solution of differential equations. Incidentally, do you consider the d. analyzer an “analogue†machine?If so, how about a polar planimeter?
My crew of NYA people has been augmented,but perhaps not for the better. The new members are fit only for adding machine work, and even then can’t get the same total more than two out of three times (so it seems!).
Here’s hoping that you have made progressin Iowa, and that I’ll get out to see it all. [PX 699]
In anticipation of his visit to Ames during the spring break, and in hopes of getting the answer to the $2 per digit question, Mauchly spent every evening in his lab looking for a solution to this most perplexing problem: if Atanasoff is using vacuum tubes in his circuits, and each vacuum-tube assembly costs $2 or more, how can he possibly produce a computer, which must certainly contain devices for storage, arithmetic, and read-out, at that price? Furthermore, since vacuum tubes operate at such tremendous speeds, the switching needed for automatic operation would also require quite a few vacuum tubes. The answer must be that one vacuum tube was being used to represent many digits. So, starting January 1, 1941, Mauchly began exploring in his lab and in circuits on paper (produced at the Honeywell trial [PX 6651) various ways of getting more information with fewer vacuum tubes.
His experiments along this line were in the design of circuits that had a digit represented by the amount of current or the amount of voltage at various places. He also tried circuits in which the digit was represented by its position in a stream of 10 pulses. For example, the number 3 could be represented by one pulse occurring in the third position in a stream of 10 pulse times. (Today this would be called pulse-position coding.)
Mauchly also wrote to General Electric for information about various tubes, particularly about the possibility of GE building for him some gas diodes that would perform better by having a greater range between their ignition voltage and their sustaining voltage.
Mauchly’s plans for getting to Iowa during the spring break fell through. Meanwhile, he continued working out his computer and constructed a number of the decade counters for it. These were, of course, the biquinary counters using gas tubes; he was eager to get something built and working.
On April 26, 1941, Mauchly wrote to H. Helm Clayton. (Mauchly had borrowed a calculator from him for use in the weather-analysis project at Ursinus.)
As our work progresses, there will be more need for reducing long series of daily values to some standard form by multiplication or division. Hence we are still thinking about and working on electrical computing circuits, as I wrote in a previous letter. Some of the simple components of an electronic computer have been constructed, and we find they work, so we are going on to the real job of putting the components together …
In June I am thinking of doing two things. One is to go to Ames, Iowa, to see an electric computing machine being developed there in the Physics Dept. by a friend of mine, and the other is to further the construction of my own devices. [Mauchly Collection]
Mauchly continued his correspondence with Atanasoff. On May 27, 1941, he wrote:
Well, anyway there is more than a little prospect of my making a trip, starting from here about the tenth of June. I have a passenger who will very likely pay for the gas,and that will help.
From your letters I have gathered that your national defense work is unconnected with your computing machine. This puzzles me, for as I understand it, rapid computation devices are involved in N.D. [national defense]. In a recent talk with Travis, of the EE School at U. of Pa., I asked him about this, and the matter seemed same way to him. But if Caldwell has looked the over your plans (I think you said he was out there) and hasn’t seen any N.D. possibilities, I suppose that means your computer is not considered adaptable to fire control devices,or that they have something even better. Travis (who goes into active duty with Navy this week) pointed out the advantages of lightness and mass-production for electronic computing methods, but said that when he was consulting with General Electric over plans for the G.E. differential integraph [differential analyzer] they figured it would take over one-half million dollars to do the job electronically, and they would spend 1/5 that, so they built the mechanical type with Polaroid torque-amplifiers. It’s too bad you couldn’t stop when you were East-but try again-no doubt you will have to come East more often. [PX 789]
Atanaoff replied on May 31, 1941.
As you may surmise, I am somewhat out of the beaten track of computing machine gossip, and so I am always interested in any details you can give me. The figures on the electronic differential integraph seem absolutely startling. ‘During Dr. Caldwell’s last visit here, I suddenly obtained an idea as to how the computing machine which we are building here can be converted into an integraph. Its action would be analogous to numerical integration, and not like that of the Bush Integraph which is, of course, an analogus [sic] machine, and the steps in the numerical integration could be made arbitrarily small. It should therefore equal the Bush machine in speed6 and excel it in accuracy.
 Progress on the construction of this machine is excellent in spite of the amount of time that defense work is taking, and I am still in a high state of enthusiasm about its ultimate success. I hope to see you within two or three weeks. [PX 794]By this time Mauchly had made sketches of many different circuits for his decade counters and their control [PX 6651. Despite all efforts at economy, while preserving reliability, he could not design a decade counter assembly that would cost him less than $13 per decade. There was no way Mauchly could personally afford to construct many decades, and Ursinus had no funds for such research. He must find another way. Mauchly at this time was uncertain of his future at Ursinus because it was becoming increasingly hard for him and his family to live on his low salary. There seemed to be lots of opportunities opening up in defense industries, so he began looking for work in electronic computing and control devices. Just before he left to visit Atanasoff he sent a letter to George Bailey in the Office of Scientific Personnel, in which he stressed his interest in computing (June 7, 1941).
I have already filled out the Specialized Personnel check lists in Physics, Statistics, and Meteorology; in each of these I indicated my interest in electrical computing devices, and electronic devices particularly. … I don’t think I qualify as an “expert†in radio engineering, but my deep interest in electronic computing and control devices is accompanied by practical laboratory work, leading now to the construction of a high-speed electronic computing circuit. Incidentally, during the next week I am going to Ames, Iowa, to visit with Dr. Atanasoff of the Iowa State Physics Dept. and to discuss with him the pros and cons of his electronic computer versus mine. [ Mauchly Collection]
Visit to Atanasoff
The only way Mauchly could afford the trip to Iowa was by having riders who would pay for the gasoline. So he arranged to drive his next-door neighbors (a farmer named Jonas Schreffler and his elderly mother) to Freeport, Illinois. He also brought along his six-year-old son, Jimmy, whose only remembrance of the long trip from Pennsylvania to Iowa in a light car over very bumpy roads was, “We just drove and drove.†Mauchly arrived at Atanasoff’s house on Friday evening, June 13. That evening they discussed (as Atanasoff has testified) “such gossip as he could bring me of computing machines from the East.†The following morning Atanasoff took him to see the machine. Here at last was the answer to the intriguing “$2 per digit.†It was a shocker! I quote from Mauchly’s testimony at the Honeywell trial, but the idea is one I heard him mention many times before that.
It was a disappointment because there had been nothing said in my meeting with him at the University of Pennsylvania which indicated that this machine was not a fully electronic machine. That’s why my great curiosity, my great wonderment, how in the world did he do this for $2 a digit, because I was thinking in terms of all-electronic things, which make use of electronic speeds. Almost immediately, of course, when I got out there, I began to learn, even though the machine was not operative, for instance, on Saturday, you could see the drum idea and you could begin to put together the picture that this is a mechanical gadget which uses some electronic tubes in operation, but it’s still restricted in speed and was not what I was interested in from the point of view of electronic speed gadgets. The fact that it was also being built specifically to solve a special class of problems, rather than a general class, was quite obvious, of course, but that wasn’t the thing that really worried me because what I had been looking for were ways of getting high-speed electronic things without paying too much for them.
Sure, this was electronic in part, but it became perfectly clear without much examination or talking that it wasn’t electronic in whole, and it was sacrificing too much of the electrical end. So I think that a lot of the conversation that we had out there was really going over this point of “Why don’t you do this or why didn’t you do that?†His machine was specifically, deliberately constructed with the idea that when finished it would solve simultaneous linear algebraic equations, which is a very special class of problems.
But there are many other problems which cannot be handled in this way and my interest was in solving some problems which couldn’t be handled this way. And I could see that other people would be interested in solving still other problems which couldn’t be handled this way. So my general interest was in trying to get computers which would be versatile and not restricted to some one class of problems. [Vol. 77, p. 11,830]
Mauchly visited the machine with Atanasoff again on Monday, and this time Clifford Berry was there to demonstrate its operation. Atanasoff has described the machine at the time of Mauchly’s visit in June 1941.
I had asked Mr. Berry to get the machine in as complete as possible form while Dr. Mauchly was visiting. I remember the main shaft was off the machine when I spoke to Clifford Berry about it, so he assembled the parts. The base 10 “card in†device was on the machine while he [Mauchly] was there. The “base 2 in†and “base 2 out†units had temporary connections while he was there. They could be mounted on the machine to indicate the mechanical arrangements here, but they were not connected underneath. We had no ability to read from a base 2 punch card at that time. [Vol. 17, p. 2434]
The “timing-control contacts†device was not in place, nor had it been designed at this time. Instead, there was a manual switch that enabled the machine to cycle one cycle.
We still had to build a number of controls, such as controls for detecting the carry through. We had to build a plus-minus recognition unit for the drum so that we could tell whether it had a plus or minus number in it. [Vol. 17, p. 2432.]
The “boost and carry drum†was designed and built after Mauchly’s visit.
At the time of Mauchly’s visit, only one drum was mounted on the shaft. The card reader was not operative so numbers were put into the machine by placing them on the drum with a charged probe. Shifting was done by hand because control apparatus was not built. [Vol. 17]
When asked about multiplication and division, Atanasoff answered,
The thing that was missing on multiplication and division on this machine was the enumerator of the count [of each addition and subtraction] so there does not appear on the output of the machine, even if it were complete, the products and divisions [quotients]. [Vol. 18, pp. 2711-2712]
The ultimate goal of the ABC (Atanasoff-Berry Computer) was to solve 29 simultaneous algebraic linear equations with 29 unknowns. The machine never accomplished this goal. A set of just five equations with five unknowns would have required the intervention of the operator over 500 times to eliminate the unknowns. The amount of operator-intervention steps increased by the cube of the number of coefficients. In the case of five equations with five unknowns, 29 or 30 steps of operator intervention were required for one reduction into the next lower equation, or about 565 steps in the solution. It took about 17 minutes of running time to do the additions and subtractions and shifts for the five simultaneous equations, exclusive of the time for the operator to put in these 500-600 steps. The amount of time for the mechanical solution on the ABC was roughly equivalent to the amount of time required to get the solution by hand. This machine could not be described as automatic. Atanasoff said,
At Dr. Mauchly’s visit the machine was in no condition to carry out a full demonstration of these steps. Quite a number of the things necessary for these steps hadn’t even been worked out. Only the function was described to Dr. Mauchly, not the details of the structure. [Vol. 19]
In the ABC the drums containing the numbers revolved at the speed of one revolution per second. The revolving drums fed the binary digits of the coefficients serially into 30 separate adder assemblies, effectively restricting the speed of the unit to one addition time per second. Mauchly puzzled over this. Why was Atanasoff using expensive vacuum tubes in the add-subtract unit when the whole advantage of them-their speed-was lost completely by the slow-moving, gear-driven drum? On the other hand, since he had the funds to buy vacuum tubes, why hadn’t he designed electronic circuits for storing his digits instead of relying on a slow mechanical rotating drum? The capacitor drum had pulse rates so slow that Atanasoff could just as well have used relays instead of vacuum tubes in his adder. Relays would have been cheaper and more reliable than Atanasoff’s adder circuits; besides, they were already developed at the time. Atanasoff admitted that although he had thought about flip-flops, he had never been able to solve the stability problem. Atanasoff testified,
I have tried to place the time of my first knowledge of it [flip-flop] and it runs in my mind that scale of two circuits and flip-flops were used for scaling cosmic rays as early as 1933. I had never used one but I saw it in the literature. Flip-flops were made to work in cosmic rays in those days, but they were sensitive to the kind of pulses they got, and the form of the pulses. The few experiments I did, and they were few, made me unhappy about that direction of approach. [Vol. 16]
The whole issue of $2 per digit Mauchly to Iowa in the first place was no unimportant. It didn’t matter how much it tremendous speed and versatility offered were not being utilized. That morning Atanasoff gave Mauchly a copy of his manuscript to read, with strict admonitions against keeping the copy or making any notes about it. A very disillusioned Mauchly glanced briefly at the manuscript and got the distinct impression that it was a proposal written to solicit funds for construction of the computer. He noticed that it contained a list of problems that used systems of algebraic linear equations, an explanation of why Atanasoff had chosen a base-two number system, and a description of the machine itself, as envisioned in August 1940. Mauchly read the paper to find out how Atanasoff had worded his “sales pitch.†Although Atanasoff’s manuscript mentions automatic control circuits, none were described in the manuscript-nor were any designed, built, or described at the time of Mauchly’s visit [Vol. 17]. Atanasoff’s patent application also mentions automatic controls (crucial elements in an automatic device) but gives no description of them. Despite repeated requests by Iowa State College, Atanasoff never supplied any drawings of these controls, and consequently no patent application was ever filed [Vol. 17, p. 2452]. No automatic programming for the ABC was planned or thought of. In a letter to Dawn Henry [Vol. 19, pp. 2894-28981, Atanasoff said: “The concept of a machine that can be programmed for any (or almost any) conceivable process was not a part of our early ideas.†The mechanical revolving drum setup precluded any branching or selection of variables. The most interesting thing about Atanasoff’s computer, from Mauchly’s point of view, was the use of condensers as memory devices. Atanasoff described their problems and how he solved them.
The trouble with condensers that they are leaky is devices and having charged a condenser,it will not stay charged, and this was the troublesome element of the era and this commenced give me concern. I came to to the conclusion that I could use condensers a memory as element by jogging their memory at regular intervals with a mechanism. The signal (on the condenser)is sensed, reconstructed, and reinserted continually as the slow shaft revolves. [Vol. 12, p. 1733]
Mauchly thought that Atanasoff’s way of “jogging the memory†was ingenious. Since Mauchly himself had been planning to use condensers as the memory element in his flip-flops, he was quite interested in seeing how someone else solved the problems with them. On Monday afternoon, Mauchly gave a talk to a group from the physics, engineering, and statistical departments of Iowa State. He talked about his work in the statistical analysis of weather data and the devices he was building and had built, such as the harmonic analyzer, for speeding up this analysis. On Tuesday Mauchly visited A. E. Brandt, a member of the statistical department for which Iowa State College was famous. Later that day he received a letter saying he had been accepted in a government-sponsored electronics course at the Moore School. In anticipation of once again becoming a student, Mauchly left with his little son early Wednesday morning, picked up his elderly passengers en route, and arrived back at Ursinus College Thursday night, June 19. Atanasoff and Berry worked on their machine for another 15 months. When asked about the condition of the machine as of September 1942, Atanasoff replied,
The “reading†part did not have a satisfactory reliability-about 95 percent-but not high enough to make the machine operative. We could not use the machine,because only way the machine could be the made usable for solving systems of equations was to get that data out after you had filled the machine and reduced the order of equations by one; then you had to punch that card out and preserve it for future operation and then put it back in the machine. The machine did not have the internal memory necessary for carrying that information. That had to be punched out in the card. Since it wasn’t available, the complete function of the machine was not available.
The last thing I remember being done to test the machine [September 1942] was the elimination of one unknown between two equations. Now, these weren’t very long equations [each equation had 4 unknowns]. No system of equations was ever solved with this machine, but towards the latter part of the period before Mr. Berry left one day we placed the coefficients of one equation on drum fl, drum CA, and another equation on drum #2, KA, and one unknown was eliminated between them, after which it was punched out on a piece of paper. [Vol. 17, p. 2445.] Mauchly wrote to Atanasoff on June 22, 1941.
I drove to Southbridge, Mass. on Friday evening. On the way back East a lot of ideas came barging into my consciousness, I haven’t had time to sift them or but organize them. They were on the subject of computing devices,of course. If any look promising, you may hear more later. [PX 816]
He wrote to Clayton on June 28,194l.
Immediately after commencement here, I went out to Iowa State University [sic] to seethe computing device which a friend of mine is constructing there. His machine, now nearing completion, is electronic in operation, and will solve within a very few minutes any system of linear equations involving no more than thirty variables. It can be adapted to do the job of the Bush differential analyzer more rapidly than the Bush machine does, and it costs a lot less.
My own computing devices use a different principle, more likely to fit small computing jobs.
While at Iowa, I talked on the construction of harmonic analyzers. But I haven’t done anything about the 27-ordinate cost-estimate as yet.
All my time since coming back from Iowa has been taken up with an Emergency Defense Training Course at the Univ. of Pa. I had a chance to teach for the summer in a defense course given to high school graduates, but turned that down in order to become a student myself. I am working in electrical engineering and electronics. Whether or not I am given a defense job involving electronics later on, the training will be helpful in connection with electronic computing devices. [PX 822]
In analyzing the situation wrote in a diary note:
I thought his [Atanasoff’s] machine was very ingenious, but since it was in part mechanical, involving rotating commutators for switching, it was not by any means what I had in mind. [Vol. 82, p. 12,493]
Meeting J. Presper Eckert at the Moore School
Mauchly began the Emergency Science and Management Defense Training Course at the Moore School on June 23,194l. There he met J. Presper Eckert, Jr., a master’s degree candidate at the Moore School who was working for the summer as lab instructor for the government-sponsored course. Since Mauchly had already done most of the experiments with his own students at Ursinus, there was free time available to exchange ideas with Eckert. The youthful Eckert (12 years younger than Mauchly) immediately impressed Mauchly with both his tremendous knowledge of electronics and his open-mindedness about what was possible with electronics. Eckert already had a patent in the television field, on a light modulator using ultrasonic waves. Mauchly described to Eckert his ideas for building a computer using pulses from electronic tubes, to get some speed. Eckert had some experience in using pulses from vacuum tubes. He thought Mauchly’s idea was indeed feasible. Eckert’s attitude and design philosophy also appealed to Mauchly. Eckert determined what he wanted to do, considered what he had to do it with, studied the peculiarities of the components, and designed the apparatus in a most conservative manner, taking all the peculiarities into account. With this design philosophy, he thought he could build reliability, the most important characteristic of a computer, into the circuits. With encouragement from Eckert that it certainly was possible to build an all-electronic digital computer using the known technology, Mauchly analyzed and clarified his thinking in one of his frequent “diary notes,†quoted in full here. Mauchly attributes the terminology analog and impulse to Atanasoff, defines an analog device, and then declines to discuss analog any further. He gives all his attention to his real interest-an electronic digital “commercial competitor for the desk type mechanical computer.†The mechanical desk calculator is still the model for Mauchly’s computer; he is still thinking of a fast, cheap, flexible vacuum-tube computer such as he was working toward at Ursinus. He talks of having multiple registers for storing data and a separate unit for the arithmetic. His ideas for automatic control are still in the formative stage.
Notes on Electrical Calculating Devices
August l5, 1941Â JWM personal diary notes
1. Analog versus impulse types. Computing machines may be conveniently classified as either “analog†or “impulse†types.*
The analog devices utilize some sort of analogue or analogy, such as Ohm’s Law or the polar planimeter mechanism, to effect a solution of a given equation. The accuracy of such devices is obviously subject to limitations; at times the attainable is more than sufficient, but there is increasing need for more computational aid not so restricted. Impulse devices comprise all those which “count†or operate upon discrete units corresponding to the integers of some number system. There is no theoretical limit to the accuracy to which such devices will work; practical limitations on the bulk or cost or convenience of operation provide the only restrictions. The usual mechanical computing machine, utilizing gears, pauls, etc., are examples of impulse calculators.
* I am indebted to Dr. J. V. Atanasoff of Iowa State College for the classification and terminology here explained.
No further attention will be given to the analog type here for although differential analyzers and other analog machines are now being used and will continue to be used for some problems, it is in the impulse machines that major improvements in speed and accuracy are to be expected and sought for.
2. For speedy (and noiseless) operation, vacuum tubes and associated circuits are the obvious answer. There are no essential differences in designing vacuum tube apparatus to do the job of ordinary mechanical calculators … but after taking care of stability, freedom from error, ease of servicing, etc. one might conceivably wind up with design too costly to build. But economically feasible designs are possible. At present it may not be possible to build a commercial competitor for the mechanical desk computer, but larger machines for more involved, more lengthy, or more specialized jobs are practical. In some cases is possible to it materially decrease number of tubes and circuits the required in a large machine by having many similar operations performed by one and the same unit, which is switched around in sequence, rather than by having many duplicate units operating simultaneously. This is possible because the time required for a single elementary operation may be very short compared to the time allowable for completing one “step†in the calculation.
3. The basic units of any computing device are usually the following: A. Input registers, for putting in (storing) the numbers to be operated on. B. The adding (or add-subtract) mechanism for combining such numbers. C. The Output register for storing, indicating, or making a permanent record of the results obtained in units A and B.
There is usually some difference in the function or form of the various registers comprising A and C. For instance, in the ordinary mechanical computing machine, a keyboard may be used to put in a multiplicand, additional buttons of a different sort may be used to put in the multiplier (which determines the number of times a multiplicand is added to each of several carriage positions), and the resulting will be read off from dial registers. These dial registers do not make any permanent record, nor can a number in that register be used immediately (without special tricks) as a multiplicand or multiplier.
In a flexible computing machine, it would be very desirable to have all the registers in which numbers may be stored immediately usable as either type A or type C. One can imagine a computing control panel such as the following. [Figure 18 is redrawn from PX 847.]
When Mauchly was writing this paper, he had not yet resigned his position as head of the Physics Department of Ursinus College, nor did he yet have any indication that his application for a teaching job at the Moore School (made at the suggestion of Carl Chambers of the Moore School staff) would be accepted. Mauchly was actively seeking work in the electronics field, and he was also hoping for an increase in salary so that, if necessary, he could afford to build his “ideal†computing devices (keyboard types) according to the plans he had laid out in the preceding memo and in an earlier memo dated August 3, 1941. Mauchly’s requirements for his “ideal†computing device-general purpose, of course-were:
A. Considerable number of registers(add to these readily).
B. Ability to transfer numbers from one register to another at will.
C. Ability to operate with number in one register on other register without losing number in original register-so that it may be used again, or checked.
D. Provision for a certain number of constant factors in machine. (A + B), or preset switches.
E. Possible automatic sequence operations with of subtotals printed (for numerical integration). F. Ten-key operation? [PX 665]
All of these requirements ultimately appeared in the ENIAC except ten-key operation. On August 18, 1941, Mauchly wrote to his wife, Mary, in Collegeville to tell her of his employment situation. He says, in part:
Chambers told me that he told the Navy man that I should get at least $4000.Chambers wouldn’t take that to go himself, of course,for he figures that his job is actually worth 10,000to him.
I asked him what he thought I might be teaching the first year. “Nothing at all,†was his answer,“-at least hardly anything. You would probably have two hours a week of circuit theory, and two or three afternoons a week in the radio laboratory. That’s all, in the first year.â€
I haven’t had a chance to sound him out as to possibility of assurance promotion. I don’t believe on that, with the one-year probation, one could get any better arrangement than that if retained I would be advanced.
At any rate, their offer will be made within a week or so,thinks Chambers,for they want to get things settled too. Two things are now known: McIlwain is on leave, rather than resigning,and the man they hoped to get for one instructor has turned down the job. He is their A-1 graduate of last year, who has landed a full time fellowship at M.I.T., and being single, is quite able to turn down larger sums for the ultimate benefit of an M.I.T. degree.
Chambers also points out that under ordinary circumstances(McIlwain’s leave is not ordinary) no staff member at Moore School has ever been let go until he found another job. The school doesn’t restrict your publication in any way, and although it has rights to patents, it always releases engineering patents to the individuals anyway, so that’s that.
Philadelphia Electric had interviews but didn’t ask me around.
But the placement man-Sweeten-who now calls me by my first name-stopped me in the hall after my GE interview and said he wanted to see me soon to talk over another possibility. He thinks that I am just the man that Dr. Bush is looking for. [Mauchly Collection]
This letter indicates that there was an opening at the Moore School that Mauchly thought he would be asked to fill, and it gives us a brief view of what Mauchly believed to be the patent policy of the Moore School. When the Moore School offered him the position as instructor, starting in September, Mauchly accepted readily. He was still hoping to build a computer, but without a lab of his own to try out his various ideas, he began writing the thoughts about circuits that were occurring to him. In a group of papers of September 1941, entitled “Computing Circuits,†he explores a number of possible computing circuits.
1. JVA’s binary condenser system adapted to decimal system (like Stibitz’s use of relays for decimal calculation). 2. Scale-of-Ten Counting Device Two condenser circuits charged with ten equal pulses, one as reference, other has pulses“suppressed.†Output is the difference in the discharge time. 3. Frequency arithmetic Adding and subtracting frequencies having different frequencies for 10 digits. 4. Modify neon tube multivibrator delay circuits for counter computer use. 5. Add time delays (a) Sawtooth step wave with changing bias (b) Pulses going any one of (10) ways according to timing; each way in succession being open, others closed. [PX 869]
Other items referred to in these early notes indicate clearly that the basic units of computation that were ultimately used in the ENIAC had already taken shape in Mauchly’s mind: a multiplier, subtraction by complement, carry-over, a master pulser, and a pulse generator. We can see these reflected in the final ENIAC. Subtraction by complement was the method used for subtraction in the decade counters of the accumulators. The “master pulse? at this time was a pulse scheme between units for controlling the sequence of events. In later work with Eckert, the “master pulse? developed into the “master programmer†for initiating programs, for subroutines, and for branching. The “cycling unit†of the ENIAC was a linear descendant of Mauchly’s “pulse generator.†Mauchly describes this period.
Well, I was continuing to actively think about and talk to others about the possibility of using entirely electronic circuits to try to accomplish calculations, computing, for any kind of scientific or engineering job. [Vol. 77, p. 11,840]
Figure 19. Moore School faculty at the Mauchly farm near Ursinus College, probably fall 1941. Front row, left to right: Jimmy Mauchly, S. Reid Warren III, Alan Warren, Jimmy Chambers, Nancy Chambers. Middle row: Mary Mauchly, Sidney Mauchly, Marion Weygandt, Margaret Morgan (now Mrs. Joseph Matlack), Marian S. Warren, Mrs. Douglas W. Mode, Margaret M. Chambers, Carol P. Brainerd. Back row: John W. Mauchly, Arthur W. Burks, Cornelius N. Weygandt, Carl C. Chambers, Rachel (Mrs. S. J.) Mauchly, John Grist Brainerd, S. Reid Warren, Jr.
As a member of the faculty, Mauchly had an opportunity to look around and talk more freely with other faculty members. He invited them to a picnic at his farm in Collegeville, where his family were still living (Figure 19).
Mauchly wanted to talk about a computer, but there were few eager listeners. Irven Travis, who had been the one most interested in computing devices and had examined the possibility of building an electronic differential integraph for GE, had left for navy duty before Mauchly had come to the electronics course in June. With the single exception of Eckert, most of the faculty and staff of the Moore School doubted that electronics (on the large scale necessary) could be made reliable enough for digital computing.
Today, few will admit to having been doubters, but at the time they had good reason for their doubts. There was nothing new about the idea of using electronic tubes for counting pulses. Chambers had worked at Bartol Research Foundation and was familiar with the binary counters that had been built there for counting cosmic rays [Vol. 821. The flip-flop had been invented in 1919. The faculty knew that vacuum tubes were notoriously unreliable, and the idea of putting a thousand of them in a single device was naive, at best, and probably foolish. Their skepticism made Mauchly sense that they were not about to consider building his electronic computer.
Furthermore, the Moore School, like all U.S. educational institutions at that time, had limited funds for research. Its main computing instrument, the Bush Differential Analyzer, had been built in 1935 with government assistance to pay machinists and draftsmen. In a joint project with Aberdeen Proving Ground, the Moore School faculty had designed and built two analyzers-one for Aberdeen and one for the Moore School-based on the design of Bush’s MIT analyzer. While the Moore School did not have to assume the total financial burden, the initiative it displayed in getting a differential analyzer for itself showed that it was obviously interested in creating and having its own computing devices.
In the fall of 1941, there was plenty of evidence that war was coming soon and that the Moore School was already being involved. Not everyone shared Mauchly’s belief that fast calculating devices would be needed. In a private communication, Irven Travis has remarked that until the end of World War II, “for the then military applications, no further speed or accuracy than that of the Bush machine was needed. Ruggedness, manufacturability, and easy maintenance were important. Primitive forerunners of electronic computers were of little interest for National defence except in certain highly classified problems.†At that time the differential analyzer was the biggest computing machine in the world and was the fastest for some major problems. It was only in retrospect, when the electromechanical differential analyzer was compared with the ENIAC, that its speed and accuracy limitations were realized by its designers and users. Mauchly could see them then, however, because he could visualize the advantages of an all-electronic digital computer. Mauchly wondered if he could interest the Moore School in building a small machine that did the work of the differential analyzer-a digital electronic replacement-perhaps funded by the government as a possible wartime project.
Mauchly remembered that Atanasoff, in his May 31, 1941, letter had said he had gotten an idea, during Samuel H. Caldwell’s last visit, for converting his (Atanasoff’s) machine into an integraph. If Atanasoff had finished building the ABC, maybe he would be free to consider building the integraph. Mauchly had some good ideas that could improve Atanasoff’s machine in speed and ease of handling. One of these was certainly electronic switching instead of mechanical switching. On September 30, 1941, Mauchly, eager to get something built, wrote to Atanasoff proposing a joint venture.
As time goes on, I expect to get a first-hand knowledge of the operation of the differential analyzer-I have already spent a bit of time watching the process of setting up and operating the thing-and with this background I hope I can outdo the analyzer electronically.
A number of different ideas have come to me recently anent computing circuits-some of which are more or less hybrids, combining your methods with other things, and some of which are nothing like your machine. The question in mind is this: Is there any objection, from your point of view, to my building some sort of computer which incorporates some of the features of your machine? For the time being, of course, I shall be lucky to find time and material to do more than make exploratory tests of some of my different ideas, with the hope of getting something very speedy, not too costly, etc.
Ultimately, a second question might come up, of course, and that is, in the event that your present design were to hold the field against all challengers, and I got the Moore School interested in having something of the sort, would the way be open for us to build an “‘Atanasoff Calculator†(a la Bush Analyzer) here? [PX 870]
When asked about this letter at the Honeywell trial, Mauchly replied:
I was still, of course, very much interested in the problems of weather and the statistical ways of dealing with them, but I was looking closely at the differential analyzer and hoping that there would [be] a way of doing what the analyzer did (solving ordinary differential equations) with electronic computing circuits. [Vol. 77]
And when asked about the Atanasoff calculator, a la Bush Analyzer), he said:
In the previous correspondence somewhere Atanasoff had told me that he had some ideas for doing this. I didn’t know exactly what his ideas were. My contact with him indicated that he was a pretty intelligent fellow who had a lot of good ideas, and also that he wasn’t always saying everything he knew; that if he didn’t tell you exactly how he was going to do it, why, it didn’t mean he didn’t know. On the other hand, it didn’t mean that he was going to tell you if he did know. So this was a sort of an open proposition, that if you got something which you think might be useful to build, perhaps the Moore School could be interested in doing this. In other words, I was looking for any kind of project that would assist calculation. It looked to me as if Moore School was a good fertile field in which to get such things supported and, after all, they had built the differential analyzer. [Vol. 77]
Atanasoff’s reply to Mauchly’s letter came the next week, October 7, 1941:
I am delighted to hear that you are teaching in the Department of Electrical Engineering at the University of Pennsylvania, and I will be sure to get in touch with you the next time I come East which should be in the very near future. At that time we can discuss our mutual interest in calculators.
Our attorney has emphasized the need of being careful about the dissemination of information about our device until a patent application is filed. This should not require too long, and of course, I have no qualms about having informed you about our device, but it does require that we refrain from making public any details for the time being. It is, as a matter of fact, preventing me from making an invited address to the American Statistical Association. [PX 899]
This letter closed the door to any chance Mauchly had for working with Atanasoff at the Moore School, and also, as Mauchly understood it, to revealing or building any hybrid of Atanasoff’s design. Mauchly had already considered (on paper) a hybrid of Atanasoff’s idea of using condensers as a cheap storage. Now, not wishing to disclose any components of the ABC, Mauchly abandoned any schemes he had recently thought of for using condensers for storage and directed his thoughts to his original (at Ursinus) ideas that were “nothing like your machine†and used only electronic elements that were not limited in their computing action by mechanical parts.
Mauchly never found out until the time of the Honeywell case that although Atanasoff and Berry worked on their calculator for another year (until September 1942), they never finished it, nor did they ever file for the patents.
As often as he could, Mauchly discussed his computer ideas with Eckert. Eckert suggested that Mauchly bring in the ring counters and other components of his computer that were still in the Physics Lab at Ursinus. Eckert tested these gas-tube circuits on a bench at the Moore School. He concluded that although gas tubes were cheap and would work for this purpose, hard vacuum tubes offered the most promise. Vacuum tubes were much more flexible in circuit design and had the added advantage of greater speed. Eckert felt that a speed of 100,000 pulses per second was practical. The most important result of this testing was the boost it gave to Mauchly’s hopes. Eckert had convinced Mauchly that it was entirely possible to build a computer having only electronic elements. There was no reason why these elements could not be used in decade ring counters as Mauchly was proposing.
Mauchly packed up his biquinary ring counters, his pulse former, and his neon flip-flops and took them home. But on his desk throughout his years at the Moore School he kept one neon flip-flop, mounted in a coffee-container lid, blinking at him (see Figure 8).
The school year 1941-1942 was a busy one for Mauchly. In addition to his teaching (see Figure 20) (in two terms he had two junior classes, two senior classes, and a year-long evening graduate class), he was employed under government contract, making calculations of radiation patterns for radar work. He continued his discussions with Eckert, who encouraged him to think about ways to get outside funding. If it were peacetime, Mauchly would have approached the Weather Bureau, because his original thoughts had been on ways to compute the weather.
During this time GE intermittently used the differential analyzer in the basement of the Moore School for problems with which faculty members were associated. Cornelius Weygandt, of the Moore School staff, demonstrated to Mauchly how the analyzer solved differential equations. Mauchly began to expand his original ideas (based on the desk calculator) and started to determine how much equipment his computer would need so that it had the capacity to solve, by numerical integration, the same problems that the differential analyzer was now solving by analog. The proposed electronic machine clearly would have many advantages over the analyzer in speed, accuracy, and flexibility. Essentially, it could solve any problem that could be solved by a person using a desk calculator.
In July 1942, the Ballistic Research Laboratory (BRL) of Aberdeen Proving Ground, by agreement with the Moore School, took over the operation of the differential analyzer for the duration of the war. Joseph Chapline, a former student of Mauchly’s at Ursinus, was hired to keep the analyzer in running condition for the Aberdeen operators. BRL sent a nucleus of computing personnel, under the direction of John V. Holberton, from Aberdeen to Philadelphia. This group trained new employees (mostly women graduates with a degree in mathematics; I was one of them) in hand computing the trajectory of a missile using desk calculators. As the need for trajectories grew, the Moore School organized formal training programs to teach new employees without degrees the background mathematics needed to do the calculations.
Mauchly lost no time in acquainting himself with the ballistics equations, how they were solved by hand, and how the differential analyzer solved them. Here he saw an immediate use and need for his automatic electronic digital calculator and an agency that might support its development. He talked this over with Chambers, who had been somewhat sympathetic if not overwhelmingly enthusiastic about such a development. Chambers advised him to write a memorandum and give it to John Grist Brainerd, who was in charge of all government contract work for the Moore School. So Mauchly phrased his August 1942 memo in terms of what an electronic computer could do for BRL.
This memo, “The Use of High Speed Vacuum Tube Devices for Calculating†(see Mauchly 1942), sets down the advantages of an electronic computer over any mechanical or electromechanical device. He states very explicitly in this memo that the components he had planned are
. . . analogous to the ordinary mechanical computing machine. . . . It is intended that this analogy shall be interpreted mechanical rather completely. . . . Just as in a computing machine the digits which represent various powers of ten are added simultaneously,so in the electronic device. . . . It is in every sense electrical analogue of the mechanical the adding, multiplying and dividing machines which are now manufactured for ordinary arithmetic purposes. However, the design of the electronic computer allows easy interconnection of a number of simple component devices.. . . The result of one calculation is immediately available for further operation in any way which is dictated by the equations governing the problem.
Here was the point of departure from all other computer devices. Mauchly is offering the possibility of subroutines. Once again, Mauchly had set down his plans for an electronic computer, this time directed toward the mathematicians at BRL. The basic design is the same one he started with at Ursinus. It is also the same one that ended up in the ENIAC. The memo deals at length with the time required for various operations, probably as a result of his discussions with Eckert. It ends with a tailored sales approach-a comparison of the time required for electronic calculation of a trajectory with the time for the same calculation by hand with a desk calculator. Mauchly discussed this memo with Louis S. Dederick, civilian chief of mathematics at BRL. Dederick answered, according to Mauchly, “It would take at least a year to build a machine like this, and by that time, the war will be over†[Vol. 78]. When army lieutenant Herman H. Goldstine, who had been assigned as liaison officer to the Moore School in the fall of 1942, heard about the memo, he asked for a copy. None could be found. A new draft was made for Goldstine from the shorthand notes of Mauchly’s secretary. Two copies of this memo were introduced as evidence in the Honeywell trial. One was Goldstine’s [PX 12251. The other, which differed slightly in wording [PX 12271, was identified as having come from Brainerd’s file. On it was a note that read:
John: Read with interest. It is easily conceivable that labor shortage may justify development work on this in the not too far distant future. J.G.B.
Many writers of the history of the ENIAC have mentioned the seemingly peculiar disappearance of this memo. I recently discussed this with Eckert, who had a very reasonable explanation. He believes that Mauchly delivered the first typed copy of the memo to Brainerd’s secretary with instructions that copies be made on the school’s only mimeograph machine and distributed to the faculty. For whatever reason, the copies were never made, and the original, with the note on it, was filed in Brainerd’s filing cabinet, not to be seen again until almost two decades later.
Goldstine’s reaction to the memo was immediate and enthusiastic. He went through the proper channels and asked Brainerd for a proposal from the Moore School. Brainerd, Eckert, and Mauchly then prepared an outline of what such a proposal should contain. They divided the work so that Brainerd wrote the introduction and general parts of the proposal, and Eckert and Mauchly produced the technical parts. Mauchly sought Eckert’s aid in writing the technical parts, thus bringing Eckert formally into the project. Eckert (1954) discusses this point.
Then the Aberdeen people-I suppose that would be Col. Gillen, who was at the Pentagon, and several other people at Aberdeen-expressed interest in this, and it was at this point that I was brought into this matter. My connection with this matter previous to that had only been informal, that I had discussed these matters with Mauchly. At that time I was brought formally into the matter because background on pulse-circuit my techniques due to the radar work had at that point advanced to more than anyone else available.
The final proposal was presented to BRL in April 1943. Its title was “Report on an Electronic Diff.* Analyzer, submitted to the Ballistic Research Laboratory, Aberdeen Proving Ground, by the Moore School of Electrical Engineering, University of Pennsylvania.†The asterisk at Diff referred to a footnote explaining why the word was abbreviated [Vol. 80, p. 12,278]. It was in the introduction to the proposal that Brainerd, despite Mauchly’s objection, introduced the term Diff. Analyzer. Mauchly felt that the name should reflect the fact that the machine was to be general purpose and in no way limited to difference equations. Colonel Paul Gillen of the Aberdeen Proving Ground suggested the name ENIAC (Electronic Numerical Integrator and Computer), and this acronym was approved by Brainerd, Goldstine, Eckert, and Mauchly. The “and Computer†was to eliminate any misunderstanding about its origins. From the beginning, the ENIAC was intended to be a general-purpose machine, even though Aberdeen’s immediate use of it would be in the solution of ballistics equations. Even before the final contract was signed, the Moore School assembled a group of engineers, and work on the ENIAC began.
Epilogue
After my marriage to Mauchly in 1948, I resigned my job at Aberdeen Proving Ground and became a full-time wife and mother to a growing family (Figure 21). Eckert and Mauchly continued as a team and together designed the EDVAC, BINAC, and UNIVAC (Figure 22). Mauchly maintained his intense interest in the use of computers, and particularly in their use in solving problems of weather, for which he collected a houseful of data and several computers of his own. Figure 23 shows Mauchly in our living room shortly before his death on January 8,198O.
- [1] Sippl, Computer Dictionary and Handbook, p. 67 (Bobbs-Merrill 1966). ↩
- [2] American National Standards Institute (ANSI), American National Dictionary for Information Processing (X-3/TR-1-77). ↩
- [3] “Mathematical Machines and Myths Concerning Their Makers or Babbage vs.
Gutenberg”, NBS Colloquium talk given by John Mauchly, Ambler, Pennsylvania, February 23, 1973. ↩ - [4] The Z3 had two predecessors: the Z1 was not programmable, and the Z2 was essentially an interim prototype for the Z3. ↩

























